Square Root Of 1 To 20
News Co
Apr 07, 2025 · 4 min read
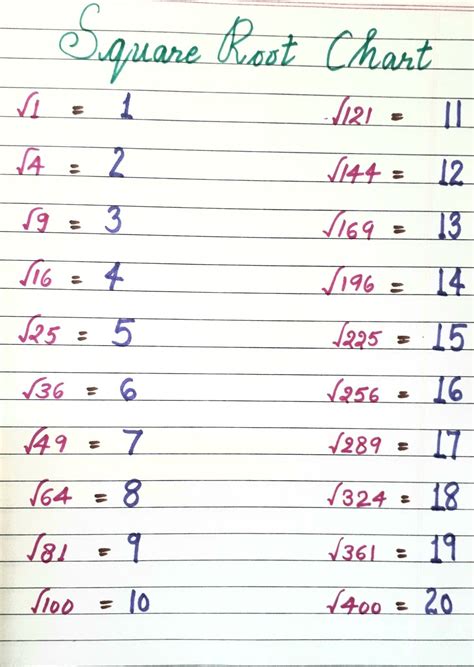
Table of Contents
Square Roots of 1 to 20: A Comprehensive Guide
Understanding square roots is fundamental to many areas of mathematics and its applications. This comprehensive guide explores the square roots of the numbers 1 through 20, delving into their properties, calculations, and practical uses. We'll move beyond simple memorization and delve into the underlying concepts, providing you with a robust understanding of this crucial mathematical concept.
What is a Square Root?
Before we dive into the specifics, let's establish a clear understanding of what a square root actually is. The square root of a number is a value that, when multiplied by itself (squared), gives the original number. For example, the square root of 9 is 3 because 3 x 3 = 9. We represent the square root using the radical symbol (√). Therefore, √9 = 3.
It's important to note that every positive number has two square roots: a positive and a negative. However, when we talk about "the" square root, we typically refer to the principal square root, which is the non-negative root.
Calculating Square Roots: Methods and Techniques
While calculating the square root of perfect squares (numbers that have whole number square roots) is relatively straightforward, finding the square root of other numbers often requires different methods.
1. Perfect Squares and Their Square Roots:
The square roots of perfect squares are whole numbers. Here's a table showing the perfect squares from 1 to 20 and their corresponding square roots:
| Number | Square Root |
|---|---|
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
These are easily memorized and are frequently used in various mathematical calculations.
2. Approximating Square Roots:
For numbers that are not perfect squares, we can approximate their square roots using several methods:
-
Estimation: By identifying the nearest perfect squares, we can make a reasonable estimate. For example, to estimate √10, we know it lies between √9 (3) and √16 (4), so the value is likely between 3 and 4, closer to 3.
-
Babylonian Method (or Heron's Method): This iterative method provides increasingly accurate approximations. The formula is: x_(n+1) = 0.5 * (x_n + S/x_n), where x_n is the current approximation, S is the number whose square root we're seeking, and x_(n+1) is the next approximation. This process is repeated until the desired accuracy is achieved.
-
Using a Calculator: Modern calculators provide a quick and accurate way to compute square roots.
Square Roots of 1 to 20: A Detailed Breakdown
Let's now delve into the square roots of each number from 1 to 20, discussing their properties and any interesting aspects:
-
√1 = 1: This is the simplest square root, representing the identity element in multiplication.
-
√2 ≈ 1.414: √2 is an irrational number, meaning it cannot be expressed as a simple fraction. It's a significant number in mathematics, appearing in many geometric and algebraic contexts.
-
√3 ≈ 1.732: Similar to √2, √3 is an irrational number with important applications in geometry and trigonometry.
-
√4 = 2: A perfect square, representing a side length of a square with an area of 4 square units.
-
√5 ≈ 2.236: Another irrational number frequently encountered in mathematical problems.
-
√6 ≈ 2.449: An irrational number.
-
√7 ≈ 2.646: An irrational number.
-
√8 ≈ 2.828: An irrational number. Note that √8 can be simplified to 2√2.
-
√9 = 3: A perfect square.
-
√10 ≈ 3.162: An irrational number.
-
√11 ≈ 3.317: An irrational number.
-
√12 ≈ 3.464: An irrational number. Can be simplified to 2√3.
-
√13 ≈ 3.606: An irrational number.
-
√14 ≈ 3.742: An irrational number.
-
√15 ≈ 3.873: An irrational number.
-
√16 = 4: A perfect square.
-
√17 ≈ 4.123: An irrational number.
-
√18 ≈ 4.243: An irrational number. Can be simplified to 3√2.
-
√19 ≈ 4.359: An irrational number.
-
√20 ≈ 4.472: An irrational number. Can be simplified to 2√5.
Applications of Square Roots
Square roots are not merely abstract mathematical concepts; they find widespread application in various fields:
-
Geometry: Calculating the length of the diagonal of a square or rectangle, the distance between two points using the Pythagorean theorem, and determining the area of a circle are just some of the instances where square roots are crucial.
-
Physics: Many physical phenomena involve square roots, including calculations related to velocity, acceleration, energy, and wave motion.
-
Engineering: In structural engineering, square roots are used extensively in calculations related to stress, strain, and stability of structures.
-
Computer Graphics: Square roots are employed in rendering and transformations for 3D modeling and animation.
-
Finance: Calculating returns on investment and understanding statistical measures often involve square roots.
-
Statistics: Standard deviation, a critical measure of data dispersion, involves the square root.
Conclusion
Understanding square roots is essential for anyone pursuing mathematics or related fields. This guide has provided a detailed exploration of the square roots of numbers 1 to 20, moving beyond simple memorization to encompass the underlying principles, calculation methods, and diverse applications of this fundamental mathematical concept. Mastering square roots provides a solid foundation for tackling more complex mathematical problems and further enhances your ability to solve problems in a wide range of scientific and practical domains. Remember to practice regularly to solidify your understanding and build confidence in your mathematical skills.
Latest Posts
Related Post
Thank you for visiting our website which covers about Square Root Of 1 To 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.