Square Root Of 2 / 2
News Co
May 08, 2025 · 5 min read
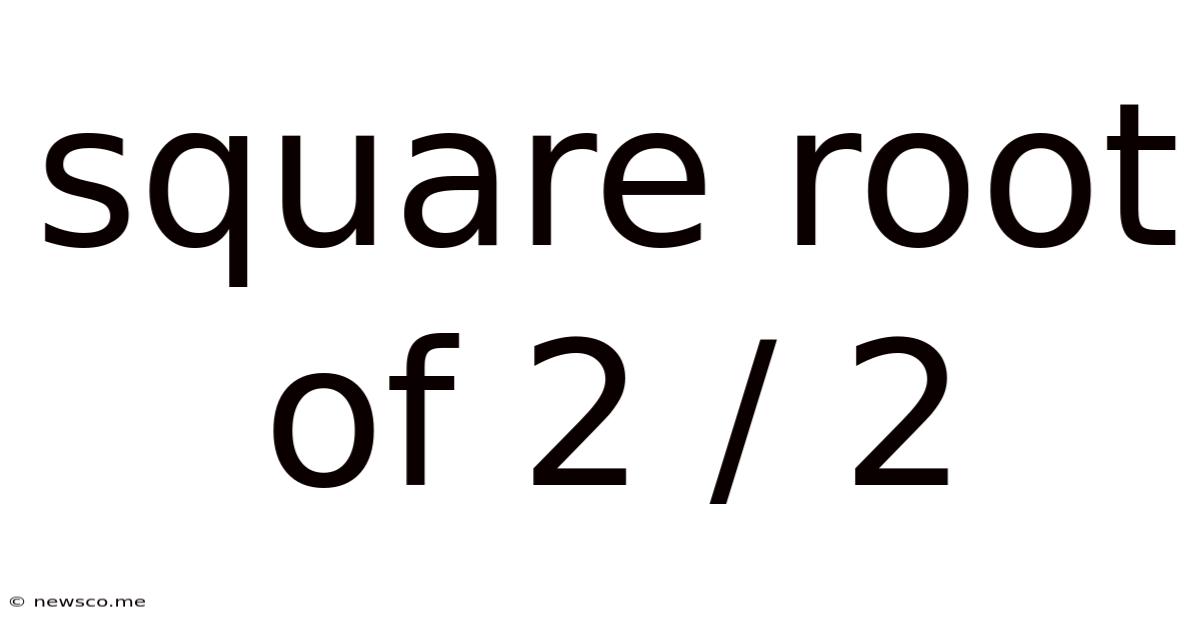
Table of Contents
Exploring the Mathematical Significance and Applications of √2/2
The seemingly simple expression √2/2, or its equivalent 1/√2, holds a significant place in mathematics and various fields of science and engineering. This article delves deep into its mathematical properties, its relationship to fundamental concepts like trigonometry and geometry, and its surprising appearances in diverse applications. We'll explore its origins, its different representations, and its crucial role in various calculations and problem-solving scenarios.
Understanding the Basics: What is √2/2?
At its core, √2/2 represents the ratio of the length of a side to the length of the hypotenuse in a 45-45-90 right-angled triangle (also known as an isosceles right triangle). In such a triangle, the two legs are equal in length, and the hypotenuse is √2 times the length of each leg. This fundamental geometric relationship is the foundation for understanding the significance of √2/2.
This ratio is also frequently expressed as 1/√2. While mathematically equivalent, the form √2/2 is often preferred as it avoids a radical in the denominator, making calculations simpler and enhancing readability in some contexts. Rationalizing the denominator, a common algebraic manipulation, transforms 1/√2 into √2/2 by multiplying both the numerator and the denominator by √2.
Decimal Representation and Approximation
The decimal approximation of √2/2 is approximately 0.70710678. This value is frequently used in practical applications where an exact value might not be necessary, or where the level of precision required can be met with a suitable approximation. However, understanding the exact mathematical representation is vital for maintaining accuracy in theoretical calculations and complex problem-solving.
Trigonometric Significance: The 45-Degree Angle
The true power of √2/2 becomes evident when we consider its connection to trigonometry. In a 45-45-90 triangle, the sine and cosine of a 45-degree angle are both equal to √2/2. This is a cornerstone relationship that underpins countless trigonometric calculations and identities.
Specifically:
- sin(45°) = √2/2
- cos(45°) = √2/2
- tan(45°) = 1 (since tan(θ) = sin(θ)/cos(θ))
This consistent appearance in trigonometric functions highlights the importance of √2/2 in solving problems involving angles of 45 degrees and their multiples. Understanding this connection is fundamental to navigation, surveying, physics, and various engineering disciplines.
Applications in Unit Circles
The unit circle, a circle with a radius of 1, is a powerful visual tool for understanding trigonometric functions. The coordinates of points on the unit circle represent the cosine and sine of the angle formed by the positive x-axis and the line connecting the origin to that point. The point corresponding to a 45-degree angle has coordinates (√2/2, √2/2), directly reflecting the values of sin(45°) and cos(45°).
Applications Across Diverse Fields
The seemingly simple √2/2 appears unexpectedly in a vast array of applications, demonstrating its fundamental importance within mathematics and its extensions into various scientific and engineering domains.
Signal Processing and Electrical Engineering
In signal processing, √2/2 plays a critical role in calculating root-mean-square (RMS) values of sinusoidal waveforms. The RMS value, often used to represent the effective value of an alternating current (AC) signal, is a crucial parameter in electrical engineering calculations. The factor √2/2 appears prominently in formulas related to power calculations and signal analysis.
Physics and Mechanics
In physics, particularly in mechanics and wave phenomena, √2/2 arises when dealing with vectors and their components at 45-degree angles. Calculations involving projectile motion, resolving forces, and analyzing wave propagation often necessitate the use of this ratio.
Computer Graphics and Game Development
In the world of computer graphics and game development, the value √2/2 is frequently utilized in rotation matrices and transformation calculations. These matrices are employed to manipulate graphical objects and characters, creating realistic movement and rotations within two-dimensional and three-dimensional spaces.
Geometry and Spatial Reasoning
Beyond trigonometry, √2/2's connection to 45-45-90 triangles makes it indispensable for solving geometric problems. Many spatial reasoning challenges involving these types of triangles require a thorough understanding of this ratio for accurate calculations and problem-solving.
Probability and Statistics
While less direct, the ratio is indirectly relevant in probability and statistics. The inherent link with the 45-degree angle and its relationship to symmetrical distributions can influence certain probability calculations involving independent events or analyzing normally distributed data.
Advanced Applications and Further Exploration
Beyond its fundamental uses, the expression √2/2 serves as a building block in more complex mathematical concepts and analyses.
Complex Numbers and Euler's Formula
When working with complex numbers, the exponential form using Euler's formula connects trigonometric functions with exponential functions. This connection further reinforces the significance of √2/2, which appears in representations of complex numbers within the complex plane.
Fourier Analysis and Signal Decomposition
Fourier analysis, a cornerstone of signal processing, uses trigonometric functions to decompose complex signals into simpler components. The value √2/2 plays a vital role in the mathematical formulations underlying this powerful technique.
Conclusion: The Enduring Importance of √2/2
The expression √2/2, while seemingly simple, represents a fundamental concept with far-reaching implications. Its appearance in trigonometry, geometry, and various scientific and engineering fields underscores its enduring importance. From its origins in the 45-45-90 triangle to its applications in advanced mathematical concepts, the ratio's consistent presence highlights its central role in shaping our understanding of the mathematical world and its applications to the real world. A deep appreciation for √2/2 enhances our ability to solve problems, analyze data, and design systems within diverse fields, making its study an essential component of a strong mathematical foundation. It's a testament to the elegance and power of mathematics that such a seemingly simple value can have such a profound and lasting impact.
Latest Posts
Related Post
Thank you for visiting our website which covers about Square Root Of 2 / 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.