Square Root Of X Times X Squared
News Co
Apr 26, 2025 · 5 min read
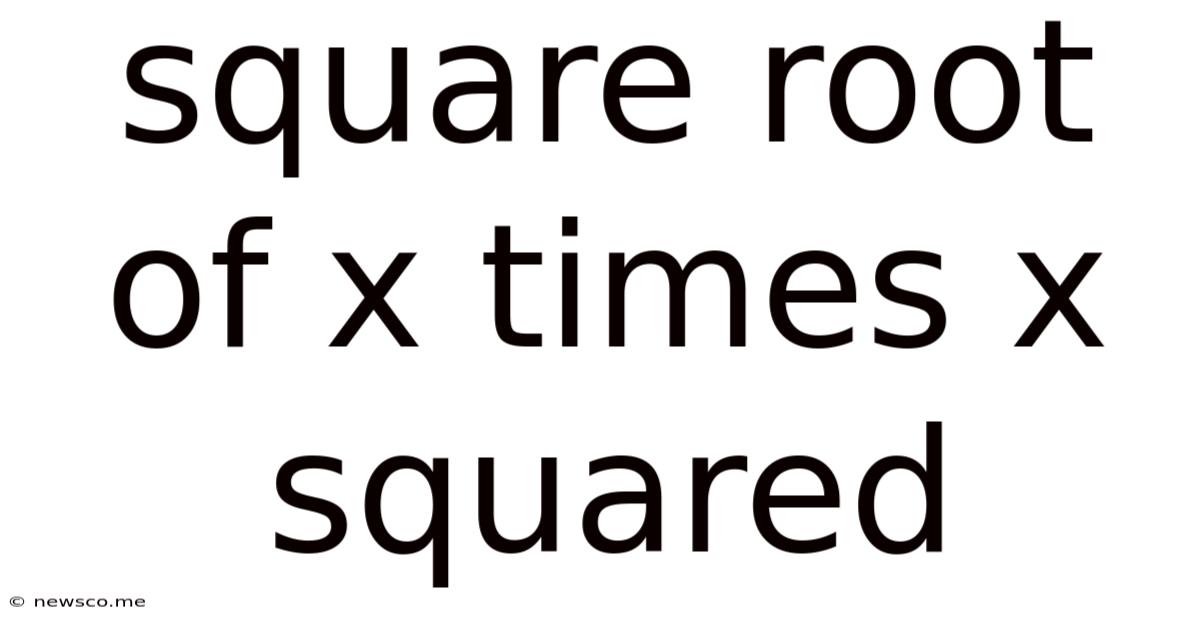
Table of Contents
Decoding the Square Root of x Times x Squared: A Deep Dive into Mathematical Concepts
The expression √x * x² might seem deceptively simple at first glance. However, understanding its simplification and the underlying mathematical principles involved requires a careful consideration of several key concepts, including exponents, radicals, and the properties of real numbers. This article will delve into a comprehensive exploration of this expression, unraveling its intricacies and highlighting its significance in various mathematical contexts.
Understanding the Fundamentals: Exponents and Radicals
Before we tackle the expression √x * x², let's solidify our understanding of the fundamental building blocks: exponents and radicals.
Exponents: The Power of Repeated Multiplication
An exponent indicates the number of times a base number is multiplied by itself. For instance, x² (x squared) means x * x. Similarly, x³ (x cubed) represents x * x * x, and so on. The exponent's value determines the power to which the base is raised.
Key Properties of Exponents:
- Product Rule: xᵃ * xᵇ = x⁽ᵃ⁺ᵇ⁾ (When multiplying terms with the same base, add the exponents.)
- Quotient Rule: xᵃ / xᵇ = x⁽ᵃ⁻ᵇ⁾ (When dividing terms with the same base, subtract the exponents.)
- Power Rule: (xᵃ)ᵇ = x⁽ᵃ*ᵇ⁾ (When raising a power to another power, multiply the exponents.)
- Zero Exponent: x⁰ = 1 (Any non-zero number raised to the power of zero equals 1.)
- Negative Exponent: x⁻ᵃ = 1/xᵃ (A negative exponent indicates the reciprocal of the base raised to the positive exponent.)
Radicals: Unveiling the Root
A radical, symbolized by √, represents a root operation. The expression √x denotes the square root of x, meaning the number that, when multiplied by itself, equals x. For example, √9 = 3 because 3 * 3 = 9. Higher-order roots, like cube roots (∛), fourth roots (∜), and so on, are also possible.
Key Properties of Radicals:
- Product Rule: √(a * b) = √a * √b (The square root of a product is the product of the square roots.)
- Quotient Rule: √(a / b) = √a / √b (The square root of a quotient is the quotient of the square roots.)
- Simplifying Radicals: Radicals are often simplified by factoring out perfect squares. For example, √12 = √(4 * 3) = √4 * √3 = 2√3.
Simplifying √x * x²: A Step-by-Step Approach
Now, let's tackle the simplification of √x * x². We can apply the properties of exponents and radicals to achieve a more concise form.
-
Rewrite the square root as a fractional exponent: Recall that √x is equivalent to x¹/². This representation is crucial for applying exponent rules.
-
Apply the Product Rule of Exponents: Our expression now becomes x¹/² * x². Since the bases are the same (x), we add the exponents: (1/2) + 2 = 5/2.
-
Result: Therefore, √x * x² simplifies to x⁵/².
This final form, x⁵/², represents the most simplified version of the original expression. It's important to note that this simplification assumes x is a non-negative real number. If x were negative, we'd need to delve into complex numbers, a more advanced mathematical realm.
Exploring Different Perspectives: Alternative Approaches
While the fractional exponent approach is arguably the most efficient, we can also explore alternative approaches to demonstrate the underlying mathematical principles.
Visualizing with Geometry
Imagine a square with side length √x. Its area would be (√x)² = x. Now, consider a rectangle with one side of length x and the other side of length x. This forms a square with area x². If we combine the area of the square (x) and the area of the rectangle (x²), we see that the original expression √x * x² represents the multiplication of the area of two geometric figures.
While this geometric approach is not a direct simplification, it offers a valuable visual interpretation of the expression.
Applying the Power Rule in Reverse
We can also approach simplification by starting from the simplified form x⁵/² and working backwards. Using the power rule in reverse, we can separate the exponent:
x⁵/² = x² * x¹/² = x²√x
This demonstrates how the simplified expression is an equivalent representation of the original expression.
Practical Applications: Where Does this Expression Appear?
The expression √x * x², or its simplified form x⁵/², appears in various mathematical and scientific contexts. Here are a few examples:
-
Calculus: This type of expression often arises during differentiation and integration, involving power functions. Understanding its simplification is fundamental for solving calculus problems efficiently.
-
Physics: In physics, particularly in areas like mechanics and electromagnetism, expressions involving fractional exponents and radicals are common. They often represent relationships between physical quantities.
-
Statistics: In statistical analysis, similar expressions may arise when dealing with distributions and probability density functions.
-
Engineering: In engineering disciplines, such as civil and electrical engineering, solving equations often involves manipulating expressions with fractional exponents and radicals.
Advanced Considerations: Domain and Range
The expression √x * x² is not defined for all real numbers. The square root operation is only defined for non-negative real numbers. Therefore, the domain of the expression is x ≥ 0. The range, however, extends to all non-negative real numbers because x⁵/² will always be non-negative for non-negative x. This understanding of domain and range is critical in analyzing the expression's behavior and its graphical representation.
Conclusion: Mastering the Fundamentals, Unlocking the Potential
The seemingly simple expression √x * x² offers a rich exploration into fundamental mathematical concepts like exponents and radicals. Through systematic simplification and careful consideration of underlying principles, we've uncovered its concise form, x⁵/². Understanding this simplification is vital for various mathematical and scientific applications. Remember to consider the domain and range of the expression to fully grasp its behavior and potential limitations. Mastering these fundamental mathematical building blocks empowers you to approach more complex problems with confidence and understanding. This comprehensive exploration provides a solid foundation for tackling future mathematical challenges.
Latest Posts
Related Post
Thank you for visiting our website which covers about Square Root Of X Times X Squared . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.