Sum Of Interior Angles In A Hexagon
News Co
Apr 06, 2025 · 5 min read
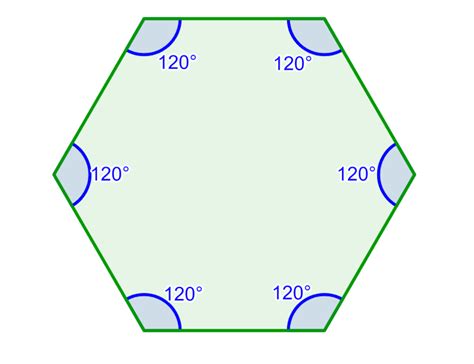
Table of Contents
The Sum of Interior Angles in a Hexagon: A Comprehensive Guide
The hexagon, a captivating six-sided polygon, holds a special place in geometry. Understanding its properties, particularly the sum of its interior angles, opens doors to solving various geometric problems and appreciating the elegance of mathematical relationships. This comprehensive guide delves into the fascinating world of hexagons, exploring different methods to calculate the sum of their interior angles and demonstrating their practical applications.
Understanding Polygons and Interior Angles
Before we dive into the specifics of hexagons, let's establish a foundational understanding of polygons and their interior angles. A polygon is a closed two-dimensional figure composed of straight line segments. These segments are called the sides of the polygon, and the points where the sides meet are called vertices. Polygons are classified based on the number of sides they possess: triangles (3 sides), quadrilaterals (4 sides), pentagons (5 sides), hexagons (6 sides), and so on.
The interior angles of a polygon are the angles formed inside the polygon at each vertex. The sum of these interior angles is a crucial characteristic of any polygon and is directly related to the number of sides it has.
Calculating the Sum of Interior Angles in a Hexagon: Method 1 - Triangulation
One of the most intuitive methods to determine the sum of interior angles in a hexagon involves dividing it into triangles. A hexagon can be divided into four triangles by drawing non-intersecting diagonals from a single vertex.
Here's how it works:
-
Draw diagonals: Start at any vertex of the hexagon and draw diagonals to the non-adjacent vertices. This will divide the hexagon into four triangles.
-
Sum of angles in a triangle: The sum of the interior angles in any triangle is always 180 degrees.
-
Total sum: Since the hexagon is divided into four triangles, the total sum of its interior angles is 4 * 180 degrees = 720 degrees.
Therefore, the sum of the interior angles in any hexagon is 720 degrees. This method beautifully demonstrates the relationship between the number of triangles and the sum of interior angles, paving the way for a more general formula.
Calculating the Sum of Interior Angles in a Hexagon: Method 2 - The General Formula
The triangulation method provides a clear understanding, but a more general formula allows for calculating the sum of interior angles for any polygon, including hexagons. This formula is based on the number of sides (n) of the polygon:
(n - 2) * 180 degrees
Where 'n' represents the number of sides. For a hexagon (n = 6), the formula becomes:
(6 - 2) * 180 degrees = 4 * 180 degrees = 720 degrees
This formula is derived from the same principle of dividing the polygon into triangles. The (n-2) term represents the number of triangles that can be formed by drawing diagonals from a single vertex.
Regular vs. Irregular Hexagons
It's important to distinguish between regular and irregular hexagons. A regular hexagon has all its sides equal in length and all its interior angles equal in measure. An irregular hexagon, on the other hand, can have sides and angles of varying lengths and measures.
While the sum of interior angles remains consistent at 720 degrees for both regular and irregular hexagons, the individual measures of each angle will differ. In a regular hexagon, each interior angle measures 720 degrees / 6 sides = 120 degrees. In an irregular hexagon, each angle can have a different measure, but their sum will always add up to 720 degrees.
Applications of the Sum of Interior Angles in Hexagons
The concept of the sum of interior angles in hexagons finds numerous applications in various fields, including:
-
Architecture and Engineering: Hexagonal structures are used in building designs, bridge construction, and honeycomb structures due to their strength and stability. Understanding the angles allows for precise construction and stress calculations.
-
Computer Graphics and Game Design: Hexagonal grids are frequently employed in game development and computer graphics for creating maps and tile-based systems. Accurate angle calculations ensure seamless tile integration and proper visual representation.
-
Tessellations and Geometry Puzzles: Hexagons are exceptional in creating tessellations (tilings that cover a surface without gaps or overlaps). The sum of interior angles plays a critical role in understanding the arrangement of hexagons to achieve complete coverage.
-
Chemistry and Crystallography: The hexagonal structure is commonly observed in various crystalline structures and chemical compounds. Understanding the angles helps in predicting the properties and behavior of these materials.
-
Cartography and Mapmaking: Hexagonal grids are increasingly utilized in cartography for representing geographic data and performing spatial analysis. Accurate angular measurements are essential for precise map creation and data representation.
Solving Problems Involving Hexagons
Let's consider a few examples to illustrate the practical application of the sum of interior angles in hexagons:
Example 1:
A regular hexagon has an interior angle of x degrees. Find the value of x.
Solution:
The sum of interior angles in a hexagon is 720 degrees. In a regular hexagon, all six angles are equal. Therefore, x = 720 degrees / 6 = 120 degrees.
Example 2:
An irregular hexagon has five interior angles measuring 110, 125, 130, 140, and 150 degrees. Find the measure of the sixth angle.
Solution:
The sum of the interior angles in any hexagon is 720 degrees. Let the sixth angle be y. Therefore:
110 + 125 + 130 + 140 + 150 + y = 720 degrees
655 + y = 720 degrees
y = 720 degrees - 655 degrees = 65 degrees
The measure of the sixth angle is 65 degrees.
Beyond the Hexagon: Exploring Other Polygons
The principles discussed for hexagons can be extended to other polygons. The general formula (n - 2) * 180 degrees applies to any polygon with 'n' sides. This formula allows us to calculate the sum of interior angles for polygons with any number of sides, reinforcing the elegant interconnectedness of geometric concepts. Understanding this fundamental principle unlocks the ability to analyze and solve problems involving a wide range of polygons.
Conclusion
The sum of interior angles in a hexagon, whether regular or irregular, is consistently 720 degrees. This fundamental concept, derived through triangulation and the general formula, underpins numerous applications across diverse fields. From architectural designs and computer graphics to chemical structures and cartography, understanding this geometric property is crucial for problem-solving and advancements in various disciplines. The exploration of hexagons, therefore, provides not just a mathematical exercise but a glimpse into the interconnectedness of mathematics and its real-world applications. By mastering this concept, we broaden our understanding of geometry and enhance our ability to approach and solve complex spatial problems.
Latest Posts
Related Post
Thank you for visiting our website which covers about Sum Of Interior Angles In A Hexagon . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.