Sum Of Interior Angles Of Hexagon
News Co
Apr 06, 2025 · 6 min read
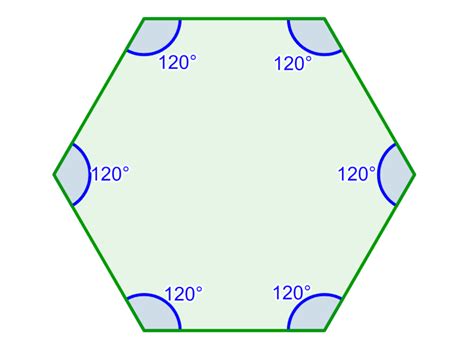
Table of Contents
The Sum of Interior Angles of a Hexagon: A Comprehensive Guide
The hexagon, a six-sided polygon, holds a fascinating place in geometry. Understanding its properties, particularly the sum of its interior angles, opens doors to a deeper appreciation of geometric principles and their applications in various fields. This comprehensive guide will delve into the calculation, proof, and applications of the sum of interior angles of a hexagon, offering a thorough understanding for students, enthusiasts, and anyone curious about this captivating geometric shape.
Understanding Polygons and Interior Angles
Before diving into the specifics of hexagons, let's establish a foundational understanding of polygons and their interior angles. A polygon is any closed two-dimensional figure formed by connecting three or more straight line segments. These segments are called the sides of the polygon. The points where the sides meet are called vertices.
Interior angles are the angles formed inside a polygon by two adjacent sides meeting at a vertex. The sum of these interior angles varies depending on the number of sides the polygon possesses. This relationship is a fundamental concept in geometry, and understanding it is key to solving numerous geometric problems.
Calculating the Sum of Interior Angles of a Hexagon
A hexagon, by definition, has six sides and six vertices. To find the sum of its interior angles, we can use a general formula applicable to all polygons. This formula is derived from dividing a polygon into triangles, a method we'll explore later in the proof section.
The formula for the sum of interior angles (S) of any polygon with 'n' sides is:
S = (n - 2) * 180°
For a hexagon, n = 6. Substituting this value into the formula, we get:
S = (6 - 2) * 180° = 4 * 180° = 720°
Therefore, the sum of the interior angles of any hexagon is always 720 degrees. This holds true regardless of the hexagon's shape – whether it's a regular hexagon (with all sides and angles equal) or an irregular hexagon (with unequal sides and angles).
Proof: Dividing the Hexagon into Triangles
The formula S = (n - 2) * 180° isn't just a rule; it's a theorem derived through a geometric proof. Let's prove this for the hexagon by dividing it into triangles:
-
Select a vertex: Choose any vertex of the hexagon.
-
Draw diagonals: From the chosen vertex, draw diagonals to all other non-adjacent vertices. For a hexagon, this will result in four triangles. Note that this method works for any polygon; the number of triangles formed will always be two less than the number of sides.
-
Sum of angles in a triangle: The sum of the interior angles in any triangle is always 180°.
-
Total sum: Since we have four triangles, the total sum of their interior angles is 4 * 180° = 720°.
-
Interior angles of the hexagon: The interior angles of the four triangles perfectly coincide with the interior angles of the hexagon. Therefore, the sum of the interior angles of the hexagon is also 720°.
This visual and logical proof demonstrates the validity of the general formula for any polygon, including the hexagon.
Types of Hexagons and their Interior Angles
While the sum of interior angles remains constant at 720° for all hexagons, the individual angles can vary depending on the type of hexagon:
-
Regular Hexagon: A regular hexagon has all six sides equal in length and all six angles equal in measure. Each interior angle of a regular hexagon measures 720° / 6 = 120°.
-
Irregular Hexagon: An irregular hexagon has sides and angles of varying lengths and measures. The sum of its interior angles will still be 720°, but the individual angle measurements will differ. The specific angles will depend on the lengths of its sides.
Understanding these distinctions is important for solving problems involving specific hexagon types.
Applications of Hexagon Geometry
Hexagons, with their unique properties, appear in various applications across multiple fields:
-
Nature: Honeycomb structures in beehives exemplify the efficiency of hexagonal geometry. Hexagons allow bees to maximize storage space using minimal materials. Similar hexagonal patterns appear in various natural formations, like basalt columns.
-
Engineering and Architecture: Hexagonal structures are often used in engineering and architecture due to their strength and stability. Hexagonal tiles are used in flooring and tiling due to their ability to tessellate perfectly, fitting together without gaps. Some buildings and bridges utilize hexagonal designs for load bearing purposes.
-
Mathematics and Computer Science: Hexagonal grids are used in computer graphics and game design, providing efficient space partitioning techniques. They find applications in cellular automata and other computational models.
Solving Problems Involving Hexagon Interior Angles
Let's explore some examples of problems involving the sum of interior angles of a hexagon:
Example 1: A hexagon has five angles measuring 110°, 120°, 130°, 140°, and 150°. What is the measure of the sixth angle?
Solution:
-
Total sum: The sum of the interior angles of any hexagon is 720°.
-
Sum of known angles: Add the measures of the five known angles: 110° + 120° + 130° + 140° + 150° = 650°
-
Measure of the sixth angle: Subtract the sum of known angles from the total sum: 720° - 650° = 70°
Therefore, the measure of the sixth angle is 70°.
Example 2: An irregular hexagon has angles measuring x, 2x, 3x, 4x, 5x, and 6x. Find the value of x.
Solution:
-
Sum of angles: The sum of the angles is x + 2x + 3x + 4x + 5x + 6x = 21x
-
Equation: Set the sum equal to 720°: 21x = 720°
-
Solve for x: Divide both sides by 21: x = 720° / 21 = 34.29° (approximately)
Therefore, the value of x is approximately 34.29°.
Advanced Concepts and Further Exploration
For those interested in delving deeper into the mathematics of hexagons, exploring these concepts would be beneficial:
-
Regular Hexagon's Properties: Investigate the properties of a regular hexagon, such as its rotational symmetry, line symmetry, and area calculations.
-
Tessellations: Explore the concept of tessellations and how hexagons contribute to creating perfectly fitting patterns without gaps.
-
Hexagonal Number System: Understand the use of hexagons in representing numbers within a unique number system.
Conclusion
The sum of interior angles of a hexagon, a constant 720°, is a fundamental concept in geometry with far-reaching applications. Understanding its calculation, proof, and practical implications provides a solid foundation for further explorations in geometry and related fields. Whether you're a student learning geometry or an enthusiast exploring mathematical concepts, mastering the hexagon's properties will enrich your understanding of the world around us. From natural formations to human-made structures, the hexagon's influence is widespread, showcasing the beauty and utility of geometric principles.
Latest Posts
Related Post
Thank you for visiting our website which covers about Sum Of Interior Angles Of Hexagon . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.