Surface Area Of A Hemisphere Calculator
News Co
Apr 07, 2025 · 6 min read
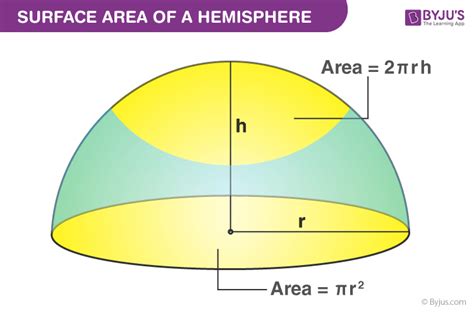
Table of Contents
Surface Area of a Hemisphere Calculator: A Comprehensive Guide
Understanding and calculating the surface area of a hemisphere is crucial in various fields, from architecture and engineering to mathematics and physics. Whether you're designing a dome, calculating the paint needed for a spherical object, or solving a complex geometry problem, knowing how to efficiently determine a hemisphere's surface area is essential. This comprehensive guide will delve into the intricacies of hemisphere surface area calculation, explore different approaches, and provide you with valuable insights into practical applications.
What is a Hemisphere?
Before diving into the calculations, let's establish a clear understanding of what a hemisphere is. A hemisphere is simply half of a sphere. A sphere is a perfectly round three-dimensional object where every point on its surface is equidistant from its center. Cutting a sphere in half through its center results in two identical hemispheres.
Understanding the Formula for Hemisphere Surface Area
The surface area of a hemisphere comprises two distinct parts:
- The curved surface area: This is the area of the curved portion, analogous to the peel of half an orange.
- The circular base area: This is the flat, circular surface at the bottom of the hemisphere.
The formula for the total surface area of a hemisphere is derived by summing these two areas:
Total Surface Area = Curved Surface Area + Base Area
Let's break down each component:
1. Curved Surface Area of a Hemisphere
The curved surface area of a hemisphere is exactly half the surface area of a complete sphere. The formula for the surface area of a sphere is 4πr², where 'r' represents the radius of the sphere. Therefore, the curved surface area of a hemisphere is:
Curved Surface Area = 2πr²
2. Base Area of a Hemisphere
The base of a hemisphere is a circle with a radius equal to the radius of the hemisphere. The formula for the area of a circle is πr². Thus, the base area of a hemisphere is:
Base Area = πr²
Combining the Areas: The Total Surface Area Formula
By adding the curved surface area and the base area, we arrive at the complete formula for the total surface area of a hemisphere:
Total Surface Area = 2πr² + πr² = 3πr²
This formula, Total Surface Area = 3πr², is the cornerstone of all hemisphere surface area calculations. Remember that 'r' always represents the radius of the hemisphere.
Using a Surface Area of a Hemisphere Calculator
While the formula is straightforward, manually performing calculations, especially with complex numbers or multiple calculations, can be time-consuming and prone to errors. This is where a dedicated hemisphere surface area calculator becomes invaluable. These online tools streamline the process, offering a quick and accurate way to determine the surface area.
Key Features of a Good Hemisphere Surface Area Calculator:
- Simple Input: A user-friendly interface that requires only the radius as input.
- Clear Output: Displays the calculated surface area clearly, ideally with units (e.g., square meters, square centimeters).
- Accuracy: Ensures precise calculations using accurate mathematical constants (π).
- Unit Conversion: Some advanced calculators might allow inputting the radius in different units (e.g., inches, feet, meters) and automatically converting the output to the desired unit.
How to Use a Hemisphere Surface Area Calculator:
The process is typically straightforward:
- Find a reliable online calculator: Search for "hemisphere surface area calculator" on a search engine.
- Input the radius: Enter the radius of the hemisphere in the designated field. Ensure you're using consistent units.
- Obtain the result: The calculator will instantly provide the calculated surface area.
Practical Applications of Hemisphere Surface Area Calculation
The calculation of hemisphere surface area finds applications in diverse fields:
1. Architecture and Engineering
- Dome design: Architects and engineers use this calculation to determine the material requirements for constructing domes, from large stadium roofs to smaller architectural features.
- Tank design: The surface area calculation is critical in designing and manufacturing spherical or hemispherical tanks for storing liquids or gases. This calculation helps in determining the amount of material needed for construction and understanding the heat transfer properties of the tank.
- Bridge construction: Hemispherical shapes are sometimes used in bridge supports and other structural components. Calculating their surface area is necessary for determining the required amount of material and for stress analysis.
2. Manufacturing and Production
- Packaging: Many products are packaged in containers with hemispherical shapes or components. The surface area calculation is essential for determining the material requirements for packaging.
- Paint and coatings: The surface area calculation is crucial for accurately determining the amount of paint or coating needed to cover a hemispherical object. This helps to prevent waste and ensure proper coverage.
- Mold making: In manufacturing processes involving molding, the surface area calculation is needed to determine the size and material requirements for molds with hemispherical cavities.
3. Science and Mathematics
- Physics: The surface area calculation is crucial for solving problems related to heat transfer, fluid dynamics, and other physical phenomena involving spherical or hemispherical objects.
- Chemistry: In chemistry, the surface area of a hemisphere can be important in calculating reaction rates for reactions that occur on surfaces, such as catalysis.
- Astronomy: The concept of surface area is vital in studying celestial objects like planets and stars, understanding their radiation and overall properties.
Advanced Considerations and Variations
While the basic formula provides a solid foundation, some situations require more advanced considerations:
1. Hemispheres with Irregular Bases
The formula 3πr² applies to hemispheres with perfectly circular bases. If the base is irregular, the calculation becomes more complex and might involve integration techniques from calculus to accurately determine the total surface area.
2. Combining Hemispheres with Other Shapes
Many real-world objects combine hemispherical shapes with other geometric forms (cylinders, cones, etc.). Calculating the total surface area requires calculating the surface area of each component separately and then summing them.
3. Accounting for Thickness
The formulas discussed assume a negligible thickness of the hemispherical shell. If the thickness is significant, the surface area calculation would need adjustments to account for the inner and outer surfaces, introducing further complexity.
Conclusion
Understanding the surface area of a hemisphere is a fundamental concept with broad practical applications. Whether you are a student, engineer, architect, or simply curious about geometry, mastering this calculation provides valuable tools for problem-solving and design. While the basic formula is simple, using a reliable hemisphere surface area calculator is highly recommended for efficiency and accuracy, especially when dealing with complex scenarios or multiple calculations. Remember to always double-check your input values and units to ensure the reliability of your results. The use of a calculator simplifies this process and allows for quicker solutions, leaving you free to focus on the larger applications of this important geometric calculation.
Latest Posts
Related Post
Thank you for visiting our website which covers about Surface Area Of A Hemisphere Calculator . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.