The Lcm Of 20 And 25
News Co
Mar 26, 2025 · 5 min read
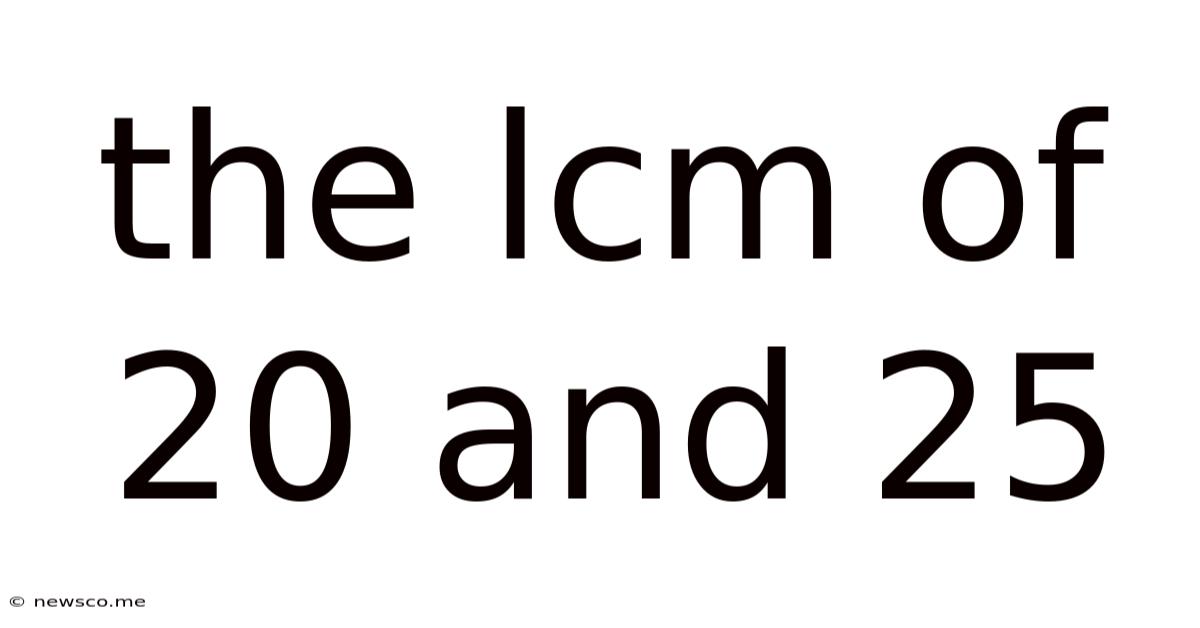
Table of Contents
Finding the Least Common Multiple (LCM) of 20 and 25: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in mathematics, particularly in number theory and algebra. Understanding how to find the LCM is crucial for various applications, from simplifying fractions to solving problems involving cyclical events. This article will delve deep into finding the LCM of 20 and 25, exploring multiple methods and illustrating the broader significance of this mathematical operation. We'll also touch upon the relationship between LCM and the greatest common divisor (GCD).
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the numbers as factors. For instance, the LCM of 2 and 3 is 6 because 6 is the smallest number divisible by both 2 and 3.
Methods to Find the LCM of 20 and 25
There are several effective methods for calculating the LCM of two numbers, and we'll explore three common approaches:
1. Listing Multiples Method
This is a straightforward method, particularly useful for smaller numbers. We list the multiples of each number until we find the smallest multiple common to both.
- Multiples of 20: 20, 40, 60, 80, 100, 120, 140, 160, 180, 200...
- Multiples of 25: 25, 50, 75, 100, 125, 150, 175, 200...
Notice that 100 appears in both lists. It's the smallest number present in both sequences, making 100 the LCM of 20 and 25. This method is effective for smaller numbers but becomes less practical as the numbers get larger.
2. Prime Factorization Method
This method is more efficient for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of all the prime factors present.
- Prime factorization of 20: 20 = 2² × 5
- Prime factorization of 25: 25 = 5²
To find the LCM, we take the highest power of each prime factor present in either factorization:
- Highest power of 2: 2² = 4
- Highest power of 5: 5² = 25
Multiplying these highest powers together gives us the LCM: 4 × 25 = 100
This method is significantly more efficient than listing multiples, especially when dealing with larger numbers. It provides a systematic and reliable approach.
3. Formula Using GCD
The least common multiple (LCM) and the greatest common divisor (GCD) of two numbers are intimately related. There's a formula that connects them:
LCM(a, b) × GCD(a, b) = a × b
Where 'a' and 'b' are the two numbers.
First, let's find the GCD of 20 and 25 using the Euclidean algorithm:
- Divide 25 by 20: 25 = 1 × 20 + 5
- Divide 20 by the remainder 5: 20 = 4 × 5 + 0
The last non-zero remainder is 5, so the GCD(20, 25) = 5.
Now, using the formula:
LCM(20, 25) × GCD(20, 25) = 20 × 25 LCM(20, 25) × 5 = 500 LCM(20, 25) = 500 / 5 = 100
This method leverages the relationship between LCM and GCD, providing another efficient way to calculate the LCM.
Applications of LCM
The LCM finds numerous applications in various fields:
1. Fraction Addition and Subtraction
Finding the LCM is essential when adding or subtracting fractions with different denominators. The LCM of the denominators becomes the common denominator, simplifying the addition or subtraction process. For example, adding 1/20 and 1/25 requires finding the LCM of 20 and 25 (which is 100), allowing us to rewrite the fractions as 5/100 and 4/100, respectively.
2. Cyclic Events
LCM is useful for solving problems involving cyclical events that repeat at different intervals. For instance, if two events occur every 20 days and 25 days respectively, the LCM (100 days) tells us when both events will occur simultaneously again.
3. Gear Ratios and Mechanical Systems
In mechanical engineering, LCM is used to calculate gear ratios and synchronize rotating parts in machinery. Understanding the LCM helps determine when different components will align perfectly.
4. Scheduling and Planning
LCM can be applied to scheduling tasks or events that recur at different intervals. For example, if two machines need maintenance every 20 and 25 days, planning the maintenance for both simultaneously requires knowing the LCM.
5. Music Theory
LCM plays a role in music theory when dealing with rhythmic patterns and musical intervals. Understanding the LCM helps in determining when different rhythmic patterns coincide.
Relationship between LCM and GCD
As demonstrated earlier, the LCM and GCD are closely related. Their product is always equal to the product of the two numbers:
LCM(a, b) × GCD(a, b) = a × b
This relationship provides a powerful tool for calculating either the LCM or GCD if the other is known. This interconnectedness highlights the fundamental role these concepts play in number theory.
Conclusion: The LCM of 20 and 25 is 100
We've explored multiple methods to determine the least common multiple of 20 and 25, consistently arriving at the answer: 100. Understanding these methods, along with the broader significance of LCM, equips you with valuable mathematical skills applicable across various disciplines. Remember that choosing the most efficient method depends on the size of the numbers involved and your familiarity with different techniques. Whether using listing multiples, prime factorization, or the LCM-GCD relationship, mastering the calculation of LCM enhances your problem-solving abilities in mathematics and beyond. The seemingly simple concept of LCM has significant implications in diverse fields, illustrating the power and elegance of fundamental mathematical principles. Further exploration of number theory can reveal even more fascinating connections and applications of LCM and related concepts.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about The Lcm Of 20 And 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.