The Sum Of 7.2 And A Number Is 10
News Co
May 07, 2025 · 5 min read
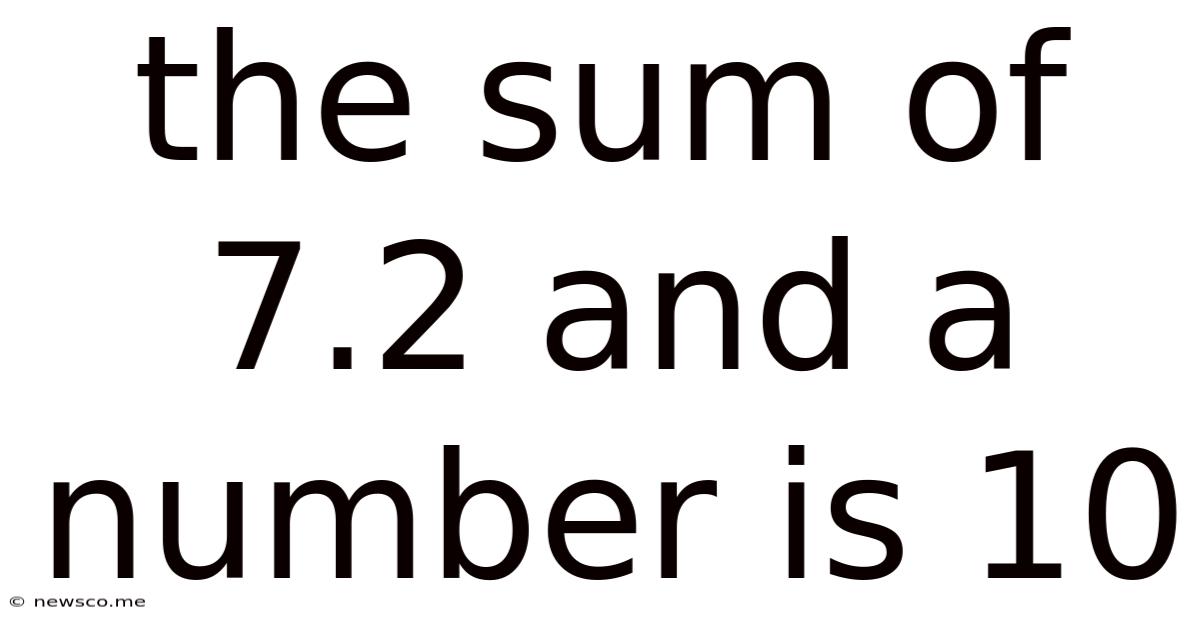
Table of Contents
The Sum of 7.2 and a Number is 10: A Deep Dive into Problem Solving and its Applications
This seemingly simple mathematical statement, "The sum of 7.2 and a number is 10," opens doors to a wide array of mathematical concepts and real-world applications. Let's explore this problem, not just to find the solution, but to understand its underlying principles and how these principles extend far beyond basic arithmetic.
Understanding the Problem: Deconstructing the Equation
The core of the problem lies in translating the sentence into a mathematical equation. The phrase "the sum of 7.2 and a number" immediately suggests addition. Let's represent the unknown number with the variable 'x'. Therefore, the equation becomes:
7.2 + x = 10
This is a simple linear equation, a fundamental concept in algebra. Solving for 'x' involves isolating the variable on one side of the equation.
Solving the Equation: Isolating the Unknown
To solve for 'x', we need to perform the inverse operation of addition, which is subtraction. We subtract 7.2 from both sides of the equation to maintain balance:
7.2 + x - 7.2 = 10 - 7.2
This simplifies to:
x = 2.8
Therefore, the unknown number is 2.8.
Verification: Checking Our Solution
A crucial step in problem-solving is verifying the solution. We substitute 'x' with 2.8 back into the original equation:
7.2 + 2.8 = 10
This confirms our solution is correct. The sum of 7.2 and 2.8 indeed equals 10.
Extending the Concept: Variations and Applications
While this specific problem is straightforward, the underlying principles have far-reaching implications. Let's explore some variations and applications:
1. Variations with Different Operations
The core concept of translating word problems into equations can be applied to problems involving subtraction, multiplication, and division. For instance:
- "The difference between a number and 7.2 is 10." This translates to x - 7.2 = 10, resulting in x = 17.2.
- "7.2 times a number is 10." This translates to 7.2x = 10, resulting in x = 10/7.2 ≈ 1.39.
- "A number divided by 7.2 is 10." This translates to x/7.2 = 10, resulting in x = 72.
2. Real-world Applications: Measurement and Finance
This basic algebraic principle forms the bedrock of countless real-world applications:
- Measurement Conversions: Converting units of measurement often involves solving similar equations. For example, converting centimeters to inches or kilograms to pounds requires applying a conversion factor, resulting in an equation that needs to be solved.
- Financial Calculations: Calculating interest, profit margins, or discounts often involves equations similar to the one we've solved. Determining the principal amount needed to reach a specific target amount after a certain interest period is a practical application of this principle.
- Scientific Calculations: Across various scientific disciplines, solving equations to find unknown variables is essential. In physics, chemistry, and engineering, many calculations involve deriving unknown quantities from known ones, echoing the approach we took in solving our original problem.
- Data Analysis: In statistics and data analysis, calculating averages, percentages, or deviations often requires solving similar equations. Understanding the underlying principles of equation solving is crucial for analyzing datasets and drawing meaningful conclusions.
3. Introducing Inequalities: Expanding the Scope
Instead of an equation (where two expressions are equal), we can also consider inequalities:
- "The sum of 7.2 and a number is greater than 10." This translates to 7.2 + x > 10, meaning x > 2.8. This introduces the concept of solution sets, where 'x' can be any number greater than 2.8.
- "The sum of 7.2 and a number is less than or equal to 10." This translates to 7.2 + x ≤ 10, meaning x ≤ 2.8. Again, this represents a solution set containing all numbers less than or equal to 2.8.
Inequalities are crucial in various fields, from determining acceptable ranges in manufacturing tolerances to understanding probability distributions in statistics.
4. More Complex Equations: Building Upon the Foundation
The principles demonstrated in solving 7.2 + x = 10 are fundamental building blocks for solving much more complex equations. These principles extend to:
- Simultaneous Equations: Solving multiple equations with multiple variables. This is vital in numerous areas, including network analysis and optimization problems.
- Quadratic Equations: Equations involving squared variables (x²). These are crucial in physics, describing projectile motion and other phenomena.
- Differential Equations: Equations involving derivatives, used extensively in modeling dynamic systems such as fluid flow and population growth.
- Advanced Mathematical Concepts: The foundation of solving linear equations is essential for understanding advanced mathematical concepts like linear algebra and calculus.
The Importance of Problem-Solving Skills: Beyond the Numbers
The seemingly simple problem, "The sum of 7.2 and a number is 10," is more than just an arithmetic exercise. It highlights the importance of:
- Analytical Thinking: Breaking down a problem into manageable parts and identifying the core elements is key to successful problem-solving.
- Mathematical Modeling: Translating a real-world scenario into a mathematical equation is a critical skill applicable across many disciplines.
- Logical Reasoning: Applying logical steps to solve an equation demonstrates deductive reasoning, a vital cognitive skill.
- Critical Thinking: Verifying the solution ensures accuracy and highlights the importance of critical evaluation in any problem-solving endeavor.
Mastering these problem-solving skills goes far beyond mathematical competence. They are transferable skills applicable to various aspects of life, from everyday challenges to complex professional tasks. They foster a structured and logical approach to tackling any problem, regardless of its complexity. The ability to approach challenges with a structured and analytical mindset is an invaluable asset in any field. The journey from a simple equation to understanding its wider applications is a testament to the power of foundational mathematical concepts and their impact on our ability to comprehend and engage with the world around us.
Latest Posts
Latest Posts
-
Vertex Of A Pair Of Congruent Angles In The Diagram
May 07, 2025
-
Which Polynomial Expression Represents A Sum Of Cubes
May 07, 2025
-
Which Bar Graph Best Represents The Provided Data
May 07, 2025
-
3 3 6 As An Improper Fraction
May 07, 2025
-
Is The Square Root Of 11 A Real Number
May 07, 2025
Related Post
Thank you for visiting our website which covers about The Sum Of 7.2 And A Number Is 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.