The Sum Of A Number And 4
News Co
May 08, 2025 · 5 min read
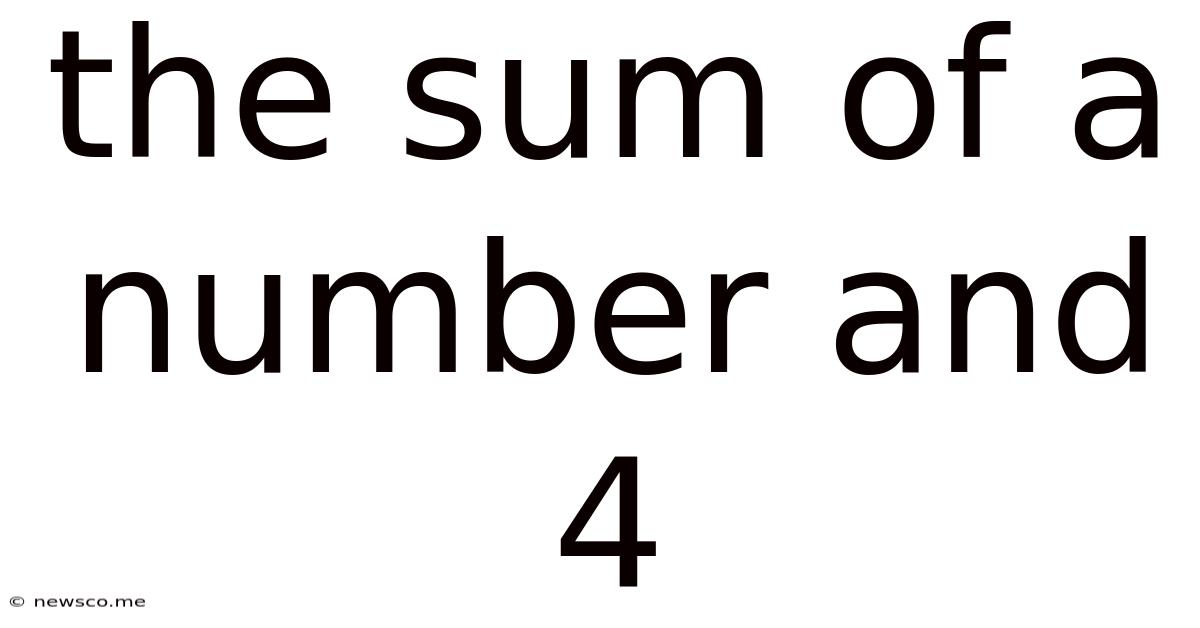
Table of Contents
The Sum of a Number and 4: A Deep Dive into Mathematical Concepts and Applications
The seemingly simple expression "the sum of a number and 4" opens a door to a vast world of mathematical concepts and practical applications. While elementary at first glance, exploring this phrase reveals fundamental principles that underpin advanced mathematical fields and real-world problem-solving. This article will delve into this seemingly simple concept, exploring its theoretical underpinnings, practical applications, and its role in shaping our understanding of mathematics.
Understanding the Fundamentals: Variables and Operations
At its core, "the sum of a number and 4" introduces two key mathematical elements: variables and operations.
Variables: Representing the Unknown
The phrase "a number" represents a variable, typically denoted by a letter such as x, y, or n. A variable is a placeholder for an unknown value. In this case, x could represent any number – positive, negative, integer, fraction, or even irrational. The beauty of using variables lies in its generality; it allows us to express a relationship that holds true regardless of the specific numerical value.
Operations: The Summation Process
The word "sum" indicates the arithmetic operation of addition. Addition is one of the four fundamental arithmetic operations, combining two or more numbers to produce a total. In our phrase, the operation is the addition of the variable (x) and the constant (4). This can be represented algebraically as: x + 4.
Algebraic Representation and Manipulation
The algebraic representation, x + 4, is crucial because it allows for mathematical manipulation and problem-solving. We can perform various operations on this expression, depending on the context of the problem.
Evaluating the Expression
If we are given a specific value for x, we can evaluate the expression. For example:
- If x = 2, then x + 4 = 2 + 4 = 6
- If x = -5, then x + 4 = -5 + 4 = -1
- If x = 0, then x + 4 = 0 + 4 = 4
- If x = 3.14, then x + 4 = 3.14 + 4 = 7.14
These examples highlight the versatility of the expression; it works consistently across different types of numbers.
Solving Equations
The expression x + 4 frequently appears within equations. An equation establishes a relationship of equality between two expressions. For instance, consider the equation:
x + 4 = 10
To solve for x, we need to isolate the variable. This involves subtracting 4 from both sides of the equation:
x + 4 - 4 = 10 - 4
This simplifies to:
x = 6
This demonstrates how the simple expression x + 4 becomes a crucial component in solving more complex mathematical problems.
Applications in Real-World Scenarios
The concept of "the sum of a number and 4" transcends the abstract realm of pure mathematics and finds practical applications in numerous real-world scenarios.
Everyday Calculations
Many everyday calculations involve adding a fixed value to a variable quantity. Consider these examples:
- Shopping: If you buy an item for x dollars and sales tax is $4, the total cost is x + 4 dollars.
- Cooking: A recipe calls for x ounces of flour, and you need to add 4 more ounces. The total amount of flour needed is x + 4 ounces.
- Travel: If a journey takes x hours, and you add a 4-hour layover, the total travel time is x + 4 hours.
These examples demonstrate the pervasiveness of this simple mathematical concept in our daily lives.
Advanced Applications: Linear Equations and Functions
The expression x + 4 forms the foundation for more advanced mathematical concepts, including linear equations and linear functions.
A linear equation is an equation that can be written in the form y = mx + b, where m is the slope and b is the y-intercept. The expression x + 4 can be considered a linear function where m = 1 and b = 4. This function represents a straight line on a graph with a slope of 1 and a y-intercept of 4.
Linear functions are ubiquitous in various fields:
- Physics: Describing the motion of objects with constant velocity.
- Economics: Modeling supply and demand relationships.
- Engineering: Representing linear relationships between variables.
Applications in Computer Science and Programming
In computer science, the concept of adding a number to another is fundamental to programming. It's a basic arithmetic operation performed constantly in various algorithms and computations.
- Looping Constructs: Adding a constant value within a loop is common in iterative processes.
- Data Manipulation: Adding values to data structures is crucial for manipulating and updating information.
Expanding the Concept: Beyond Simple Addition
While we've focused on the basic expression x + 4, the core concept of adding a constant value to a variable extends to more complex scenarios.
Adding Multiple Constants
We could easily expand the concept to include multiple constants: x + 4 + 7, for instance. This involves performing multiple additions to arrive at a final sum.
Adding Variables
The concept extends beyond adding a constant to a single variable. Consider expressions such as: x + y + 4, where both x and y are variables. This introduces the concept of multiple variables and their combined sum.
Functions and Transformations
In advanced mathematics, functions are used to transform variables. Consider a function f(x) = x + 4. This function takes an input value (x) and transforms it by adding 4 to produce an output value. This concept of functional transformations is crucial in various branches of mathematics and computer science.
Conclusion: The Significance of Simple Concepts
The seemingly simple expression "the sum of a number and 4" provides a powerful introduction to core mathematical concepts. From the fundamental principles of variables and operations to its applications in solving equations, modeling real-world scenarios, and forming the basis for more advanced concepts, this expression highlights the importance of understanding even the most basic mathematical building blocks. Its versatility and widespread applicability underline its significance in mathematics, computer science, and various other fields. The seemingly simple act of adding 4 to a number opens doors to a vast and fascinating world of mathematical possibilities. Mastering this fundamental concept lays a strong foundation for understanding more complex mathematical structures and solving increasingly intricate problems.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about The Sum Of A Number And 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.