True Or False All Squares Are Rectangles
News Co
Apr 14, 2025 · 5 min read
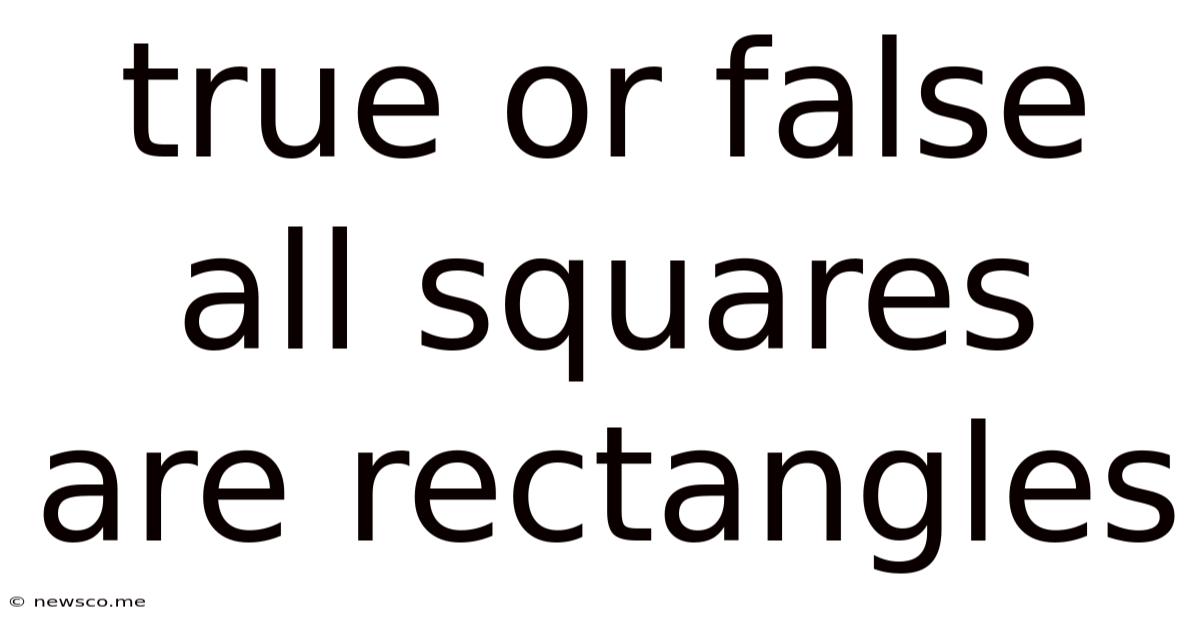
Table of Contents
True or False: All Squares are Rectangles
The question, "Are all squares rectangles?" often sparks debate, especially among geometry enthusiasts. The answer, however, is a definitive true. Understanding why requires delving into the fundamental definitions of squares and rectangles, exploring their properties, and examining the hierarchical relationship between these two quadrilaterals. This article will thoroughly explore this geometrical truth, providing a comprehensive explanation suitable for students, educators, and anyone curious about the fascinating world of geometry.
Understanding the Definitions: Squares and Rectangles
Before we definitively answer the question, let's establish clear definitions for both squares and rectangles. This is crucial because a firm grasp of these definitions forms the bedrock of our understanding.
What is a Rectangle?
A rectangle is a quadrilateral (a four-sided polygon) possessing the following characteristics:
- Four right angles: Each of its internal angles measures exactly 90 degrees.
- Opposite sides are equal and parallel: The lengths of opposite sides are congruent (equal in length), and these sides are parallel to each other.
These two properties are the defining characteristics of a rectangle. Any quadrilateral that satisfies both conditions is classified as a rectangle.
What is a Square?
A square is also a quadrilateral, but it possesses a more specific set of properties:
- Four right angles: Just like a rectangle, all its internal angles measure 90 degrees.
- Four equal sides: All four sides are congruent (equal in length).
- Opposite sides are parallel: Similar to a rectangle, opposite sides are parallel to each other.
Notice that the definition of a square includes all the properties of a rectangle, plus the additional constraint that all four sides must be equal. This is the key to understanding the relationship between squares and rectangles.
The Hierarchical Relationship: Why All Squares are Rectangles
Because a square possesses all the properties of a rectangle (four right angles and opposite sides that are equal and parallel), it inherently is a rectangle. Think of it as a hierarchical relationship:
- Quadrilaterals: This is the broadest category, encompassing all four-sided polygons.
- Rectangles: A subset of quadrilaterals characterized by four right angles and opposite sides that are equal and parallel.
- Squares: A subset of rectangles, inheriting all rectangular properties and adding the constraint of equal side lengths.
This means that every square is a rectangle, but not every rectangle is a square. This is a crucial distinction. The property of having equal sides is what differentiates a square from other rectangles.
Visualizing the Relationship: Venn Diagrams and Set Theory
A Venn diagram effectively illustrates this hierarchical relationship. Imagine two overlapping circles:
- Circle 1: Rectangles This circle represents all shapes that are rectangles.
- Circle 2: Squares This circle represents all shapes that are squares.
Since all squares are rectangles, the circle representing squares is completely contained within the circle representing rectangles. There is no part of the square circle that lies outside the rectangle circle. This visually demonstrates that the set of squares is a subset of the set of rectangles.
This concept aligns perfectly with set theory, where the set of squares is a proper subset of the set of rectangles. This formal mathematical representation reinforces the geometrical truth.
Common Misconceptions and Clarifications
The confusion often arises from focusing on the additional property of a square (equal sides) rather than the inclusive properties. Some might argue that because a square has extra properties, it cannot be considered a rectangle. However, this reasoning is flawed. Possessing additional properties doesn't negate the presence of the defining characteristics of a rectangle.
Think of it like this: A human is a mammal, a vertebrate, and an animal. Each classification encompasses the properties of the previous ones. Being a vertebrate doesn't preclude someone from being a mammal or an animal. Similarly, having equal sides doesn't disqualify a square from being a rectangle.
Exploring Real-World Applications and Examples
The understanding of this geometrical relationship has practical implications in various fields:
- Engineering and Architecture: Designing structures often involves working with rectangles and squares. Knowing that a square is a specific type of rectangle simplifies calculations and design processes.
- Computer Graphics and Programming: Representing shapes and objects in computer graphics relies heavily on geometrical principles. Understanding the relationship between squares and rectangles allows for efficient coding and representation.
- Education: Teaching this concept enhances problem-solving skills and fosters a deeper understanding of geometrical relationships.
Further Exploration: Other Quadrilaterals and Their Relationships
Understanding the relationship between squares and rectangles lays a strong foundation for exploring other quadrilaterals and their interrelationships. For example:
- Rhombus: A rhombus is a quadrilateral with all four sides equal in length. Unlike a square, it doesn't necessarily have right angles.
- Parallelogram: A parallelogram is a quadrilateral with opposite sides parallel. Rectangles and rhombuses are specific types of parallelograms.
- Trapezoid: A trapezoid is a quadrilateral with at least one pair of parallel sides.
Exploring these relationships helps build a comprehensive understanding of quadrilateral geometry. The hierarchical structure, similar to the square-rectangle relationship, allows for a systematic approach to understanding the properties and classifications of different quadrilaterals.
Conclusion: A Fundamental Geometrical Truth
The statement "All squares are rectangles" is unequivocally true. This truth stems from the fundamental definitions of these shapes and their inherent properties. A square satisfies all the requirements to be classified as a rectangle, plus the additional constraint of having equal sides. This hierarchical relationship, easily visualized through Venn diagrams and supported by set theory, is crucial for a thorough understanding of geometry. This knowledge has practical applications in various fields and serves as a cornerstone for further exploration of geometrical concepts and relationships. Understanding this seemingly simple truth lays a solid foundation for advanced geometrical studies and problem-solving.
Latest Posts
Related Post
Thank you for visiting our website which covers about True Or False All Squares Are Rectangles . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.