Twenty-one Is 35 Of What Number
News Co
May 08, 2025 · 5 min read
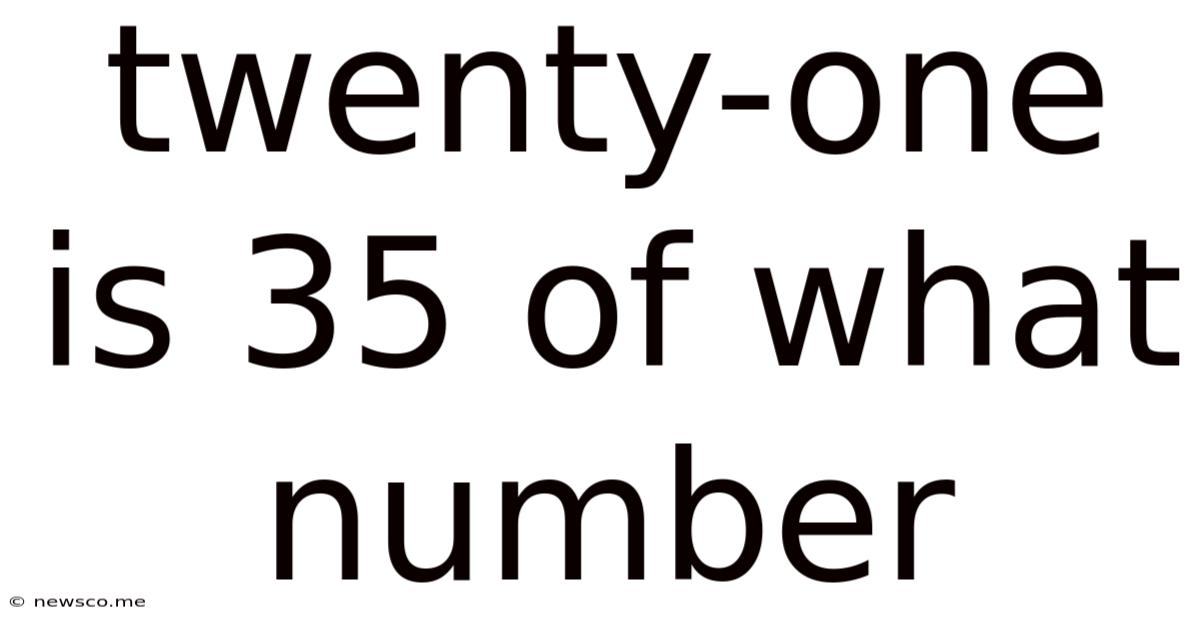
Table of Contents
Twenty-One is 35% of What Number? A Comprehensive Guide to Percentage Calculations
This article delves deep into the question: "Twenty-one is 35% of what number?" We'll not only solve this specific problem but also equip you with the knowledge and techniques to tackle any percentage calculation with confidence. We’ll explore various methods, from basic algebraic solutions to practical applications and real-world examples. By the end, you’ll be a percentage problem-solving pro!
Understanding Percentages
Before diving into the solution, let's solidify our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. For example, 35% means 35 out of 100, which can be written as the fraction 35/100 or the decimal 0.35. Understanding this fundamental concept is crucial for solving percentage problems.
Key Percentage Terminology
- Percentage (%): Represents a portion of a whole, expressed as a number out of 100.
- Base: The whole or original amount. This is the number we are finding a percentage of.
- Part: The portion of the base represented by the percentage.
- Rate: The percentage itself (e.g., 35%).
Solving "Twenty-One is 35% of What Number?"
Now, let's tackle the problem at hand. We know the part (21) and the rate (35%). We need to find the base. We can represent this mathematically using the following equation:
Part = Rate × Base
Substituting the known values:
21 = 0.35 × Base
To solve for the base, we need to isolate it. We can do this by dividing both sides of the equation by 0.35:
Base = 21 / 0.35
Calculating this gives us:
Base = 60
Therefore, twenty-one is 35% of 60.
Alternative Methods for Solving Percentage Problems
While the above method is straightforward, several other approaches can be used to solve percentage problems. Let's explore a few:
Method 2: Using Proportions
We can set up a proportion to solve this problem:
21/x = 35/100
Where 'x' represents the unknown base. Cross-multiplying, we get:
21 * 100 = 35 * x
2100 = 35x
x = 2100 / 35
x = 60
This method confirms our previous result. Setting up proportions is particularly useful when dealing with more complex percentage problems.
Method 3: Working with Fractions
We can convert the percentage to a fraction and solve accordingly:
35% = 35/100 = 7/20
The equation becomes:
21 = (7/20) * Base
Multiply both sides by 20/7 to isolate the base:
Base = 21 * (20/7)
Base = 3 * 20
Base = 60
Practical Applications and Real-World Examples
Percentage calculations are ubiquitous in everyday life. Here are some examples illustrating their practical applications:
- Discounts: A store offers a 35% discount on an item originally priced at $60. The discount amount is 35% of $60, which is $21 ($60 * 0.35 = $21). The sale price would be $39 ($60 - $21 = $39).
- Taxes: If a sales tax is 6%, and you purchase an item for $100, the tax amount would be 6% of $100, which is $6 ($100 * 0.06 = $6). The total cost would be $106.
- Tips: Calculating tips in restaurants often involves percentages. A 15% tip on a $50 meal would be $7.50 ($50 * 0.15 = $7.50).
- Interest Rates: Banks use percentages to calculate interest on savings accounts and loans. If your savings account earns 2% interest annually on a balance of $1000, you’ll earn $20 in interest ($1000 * 0.02 = $20).
- Grade Calculations: Your final grade in a course is often calculated as a weighted average of different assignments and exams, using percentages to reflect the importance of each component.
Advanced Percentage Problems and Techniques
While the problem we initially tackled was relatively simple, percentage problems can become more complex. Let's look at some scenarios requiring more advanced techniques:
Calculating Percentage Increase or Decrease
Suppose a quantity increases from 50 to 60. To calculate the percentage increase, we first find the difference (60 - 50 = 10). Then, we divide this difference by the original amount and multiply by 100:
(10/50) * 100 = 20%
Therefore, there was a 20% increase. Percentage decrease is calculated similarly, but the difference is divided by the original amount.
Solving for the Rate or the Part
We've already solved for the base. However, you might be given the base and the part, and asked to find the percentage rate or vice-versa. The same fundamental formula (Part = Rate x Base) applies, but you'll need to rearrange it to solve for the unknown variable.
Multiple Percentage Changes
Sometimes, you'll encounter scenarios involving multiple percentage changes. For instance, an item is discounted by 20% and then further discounted by 10%. You cannot simply add the percentages (30%) because the second discount is applied to the already reduced price. You must calculate each discount sequentially.
Mastering Percentage Calculations: Tips and Tricks
- Practice regularly: The more you practice solving percentage problems, the more comfortable and proficient you'll become.
- Understand the concept: Ensure you understand the fundamental principles of percentages before attempting complex problems.
- Use different methods: Explore various approaches (algebraic, proportions, fractions) to find the method that best suits your understanding and the problem at hand.
- Check your work: Always verify your answer using a different method or by estimating the result.
- Utilize online calculators and resources (for verification only): While you should aim to solve problems manually to improve your understanding, online calculators can serve as useful tools for checking your answers. However, avoid relying on them solely, as understanding the underlying principles is crucial.
Conclusion: Embracing the Power of Percentages
Understanding and mastering percentage calculations is essential for navigating various aspects of daily life, from personal finance to academic pursuits and professional settings. This comprehensive guide provides a solid foundation for tackling percentage problems of varying complexities. Remember that practice and a thorough understanding of the underlying concepts are key to achieving proficiency. By applying the techniques and methods discussed here, you'll confidently solve any percentage problem that comes your way.
Latest Posts
Latest Posts
-
Find The Slope Given Two Points Worksheet
May 08, 2025
-
What Is 40 Of An Hour
May 08, 2025
-
Which Of The Following Statements About The Mean Are True
May 08, 2025
-
What Does The Word Per Mean In Math
May 08, 2025
-
The Top Number Of A Fraction
May 08, 2025
Related Post
Thank you for visiting our website which covers about Twenty-one Is 35 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.