Two Parallel Lines Are Cut By A Transversal
News Co
Apr 03, 2025 · 6 min read
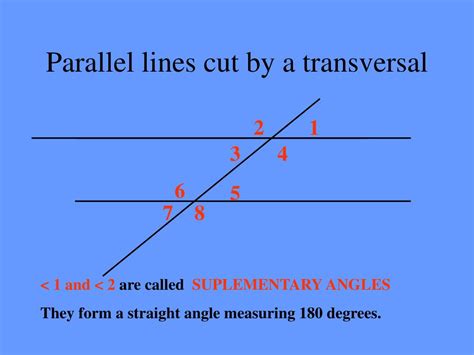
Table of Contents
Two Parallel Lines Cut by a Transversal: A Comprehensive Guide
When two parallel lines are intersected by a transversal line, a fascinating array of geometric relationships emerges. Understanding these relationships is crucial in geometry, and has practical applications in various fields like architecture, engineering, and even art. This comprehensive guide will delve into the properties and theorems associated with this fundamental geometric configuration. We'll explore the angles formed, prove key theorems, and showcase practical examples to solidify your understanding.
Understanding the Basics
Before diving into the intricacies, let's establish some fundamental terminology.
-
Parallel Lines: Two lines are parallel if they lie in the same plane and never intersect, no matter how far they are extended. We often denote parallel lines using symbols like l ∥ m.
-
Transversal Line: A transversal line is a line that intersects two or more other lines at distinct points. In our case, it intersects two parallel lines.
-
Angles Formed: The intersection of two parallel lines and a transversal creates eight angles. These angles are categorized into various types:
- Interior Angles: Angles that lie between the two parallel lines.
- Exterior Angles: Angles that lie outside the two parallel lines.
- Consecutive Interior Angles: Interior angles that are on the same side of the transversal.
- Alternate Interior Angles: Interior angles that are on opposite sides of the transversal.
- Corresponding Angles: Angles that are in the same relative position at the intersection of the transversal and each parallel line.
Key Theorems and Their Proofs
The relationships between the angles formed when two parallel lines are cut by a transversal are governed by several important theorems. Let's explore these theorems and provide rigorous proofs:
1. Corresponding Angles Theorem
Statement: If two parallel lines are cut by a transversal, then corresponding angles are congruent.
Proof:
Consider two parallel lines, l and m, intersected by a transversal line, t. Let's label the angles formed as shown in the diagram below. (Note: I can't create visual diagrams here, but imagine a diagram with two parallel lines l and m, crossed by transversal t, resulting in 8 labeled angles).
We want to prove that ∠1 ≅ ∠5, ∠2 ≅ ∠6, ∠3 ≅ ∠7, and ∠4 ≅ ∠8.
We can use a proof by contradiction. Assume, for the sake of contradiction, that ∠1 ≠ ∠5. If ∠1 and ∠5 are not congruent, then the lines l and m would intersect, contradicting our initial assumption that l and m are parallel. Therefore, corresponding angles must be congruent. A similar argument can be applied to the other pairs of corresponding angles.
2. Alternate Interior Angles Theorem
Statement: If two parallel lines are cut by a transversal, then alternate interior angles are congruent.
Proof:
Using the same diagram as above, we want to prove that ∠3 ≅ ∠6 and ∠4 ≅ ∠5.
Notice that ∠3 and ∠1 are supplementary angles (they add up to 180°). Similarly, ∠6 and ∠1 are corresponding angles, and thus congruent (by the Corresponding Angles Theorem). Since ∠3 and ∠1 are supplementary, and ∠1 and ∠6 are congruent, it follows that ∠3 and ∠6 are congruent. A similar argument can be made to show that ∠4 ≅ ∠5.
3. Consecutive Interior Angles Theorem
Statement: If two parallel lines are cut by a transversal, then consecutive interior angles are supplementary.
Proof:
We want to prove that ∠3 + ∠5 = 180° and ∠4 + ∠6 = 180°.
From the Corresponding Angles Theorem, we know that ∠1 ≅ ∠5. Since ∠1 and ∠3 are supplementary (they form a linear pair), we have ∠1 + ∠3 = 180°. Substituting ∠5 for ∠1, we get ∠5 + ∠3 = 180°. A similar argument applies to the pair ∠4 and ∠6.
4. Converse Theorems
The converse of each of the above theorems is also true. For example, the converse of the Corresponding Angles Theorem states: If two lines are cut by a transversal and corresponding angles are congruent, then the lines are parallel. Similar converse statements hold for the Alternate Interior Angles Theorem and the Consecutive Interior Angles Theorem. The proofs of these converse theorems often utilize indirect proof (proof by contradiction).
Applications and Real-World Examples
The principles governing parallel lines cut by a transversal aren't just abstract mathematical concepts; they have numerous practical applications:
- Architecture and Construction: Architects and engineers use these principles to ensure structural stability and precision in building design. Parallel lines and transversals are essential in creating accurate blueprints and ensuring that walls, floors, and roofs are properly aligned.
- Civil Engineering: Road design often involves parallel lines representing lanes, and transversals representing intersections. Understanding angle relationships is critical for safe and efficient road layouts.
- Graphic Design: In creating visually appealing designs, understanding the relationships between angles can help in creating symmetry and balance. Parallel lines and transversals can be utilized in creating patterns and repeating elements in designs.
- Carpentry and Woodworking: Precision in carpentry relies on accurate angle measurements. Understanding parallel lines and transversals is essential for creating joints, cutting angles, and ensuring structural integrity in woodworking projects.
- Computer Graphics: In computer-aided design (CAD) software and 3D modeling, the principles of parallel lines and transversals are fundamental for creating accurate and consistent representations of objects and scenes.
Beyond the Basics: Exploring More Complex Scenarios
While the basic theorems cover the most common scenarios, more complex situations can arise when dealing with multiple parallel lines and transversals. For example:
- Multiple Parallel Lines: If three or more parallel lines are intersected by a transversal, the same angle relationships hold true for each pair of parallel lines.
- Multiple Transversals: If two parallel lines are intersected by multiple transversals, the resulting angles will exhibit consistent relationships, facilitating complex geometric problem-solving.
These more complex scenarios often require a combination of the fundamental theorems to solve for unknown angles or prove specific geometric relationships.
Problem Solving Strategies
Solving problems involving parallel lines cut by a transversal often involves:
-
Identifying Parallel Lines and Transversals: Clearly identify which lines are parallel and which line acts as the transversal.
-
Labeling Angles: Label all the angles formed, using consistent notation.
-
Applying Theorems: Determine which theorems apply based on the given information and the angles you need to find.
-
Setting up Equations: Write equations based on the relationships between the angles (congruence, supplementary angles).
-
Solving Equations: Solve the equations to find the values of unknown angles.
-
Verifying Solutions: Ensure your solutions are consistent with the properties of parallel lines and transversals.
Conclusion
The intersection of two parallel lines by a transversal forms a rich and important area of study in geometry. The theorems presented here provide a solid foundation for understanding the angle relationships that arise in this configuration. Mastering these concepts is crucial not just for success in geometry, but also for practical applications in various fields that rely on precise measurements and geometric understanding. By understanding the theorems and practicing problem-solving, you can gain a deeper appreciation for the elegant simplicity and widespread utility of this fundamental geometric concept.
Latest Posts
Related Post
Thank you for visiting our website which covers about Two Parallel Lines Are Cut By A Transversal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.