Volume Of A Rectangular Pyramid Calculator
News Co
Apr 05, 2025 · 5 min read
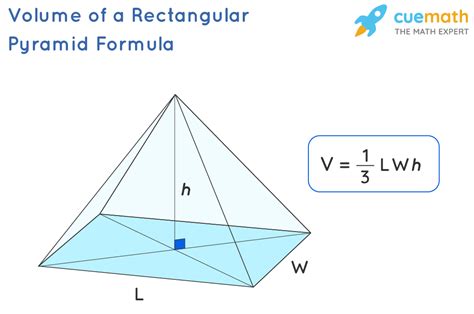
Table of Contents
Volume of a Rectangular Pyramid Calculator: A Comprehensive Guide
Understanding how to calculate the volume of a rectangular pyramid is crucial in various fields, from architecture and engineering to surveying and even game development. While manual calculations are possible, using a volume of a rectangular pyramid calculator offers speed, accuracy, and convenience. This comprehensive guide explores the intricacies of rectangular pyramid volume calculation, delves into the practical applications of such calculations, and provides insights into leveraging online calculators effectively.
Understanding Rectangular Pyramids
Before we dive into the calculations, let's solidify our understanding of rectangular pyramids. A rectangular pyramid is a three-dimensional geometric shape characterized by:
- A rectangular base: The foundation of the pyramid is a rectangle. The dimensions of this rectangle (length and width) are critical for volume calculation.
- Triangular sides: Four triangular faces rise from the sides of the rectangular base, converging at a single point called the apex or vertex.
- Height: The perpendicular distance from the apex to the base plane is known as the height (or altitude) of the pyramid. This is also crucial for volume calculations.
It's important to distinguish a rectangular pyramid from other pyramids (like square pyramids or triangular pyramids), as the base shape dictates the formula used for volume calculations.
The Formula: Calculating the Volume
The formula for calculating the volume (V) of a rectangular pyramid is:
V = (1/3) * l * w * h
Where:
- l represents the length of the rectangular base.
- w represents the width of the rectangular base.
- h represents the height of the pyramid.
This formula signifies that the volume is one-third the volume of a rectangular prism (cuboid) with the same base and height. This is a fundamental concept in geometry, relating the volumes of these 3D shapes.
Step-by-Step Manual Calculation
Let's illustrate the manual calculation with an example. Consider a rectangular pyramid with:
- Length (l) = 10 cm
- Width (w) = 5 cm
- Height (h) = 8 cm
Following the formula:
- Multiply length and width: 10 cm * 5 cm = 50 cm² (This gives us the area of the rectangular base).
- Multiply by the height: 50 cm² * 8 cm = 400 cm³
- Multiply by 1/3: (1/3) * 400 cm³ = 133.33 cm³ (approximately)
Therefore, the volume of this rectangular pyramid is approximately 133.33 cubic centimeters.
The Advantages of Using a Volume of a Rectangular Pyramid Calculator
While manual calculation is straightforward for simple examples, it becomes time-consuming and prone to errors with more complex problems involving decimal values or larger numbers. This is where a dedicated online calculator shines. The advantages include:
- Speed and Efficiency: Calculators instantly provide the result, saving valuable time, especially when dealing with numerous calculations.
- Accuracy: Calculators minimize the risk of human error in calculations, ensuring precise results.
- Ease of Use: Most calculators have user-friendly interfaces, requiring minimal input of data. You simply enter the length, width, and height, and the calculator does the rest.
- Handling Complex Numbers: Calculators effortlessly handle decimal values, fractions, and large numbers, making calculations much easier.
- Educational Tool: Calculators can be used as a learning tool alongside manual calculations to check answers and deepen understanding.
Choosing the Right Online Calculator
When searching for a volume of a rectangular pyramid calculator, consider these factors:
- User Interface: Look for a calculator with a clear, intuitive interface that is easy to navigate and understand.
- Accuracy: Ensure the calculator provides accurate results. You can cross-check the results with manual calculations for a few test cases.
- Additional Features: Some calculators may offer additional features, such as unit conversion (e.g., converting cubic centimeters to cubic meters) or the ability to save calculations.
- Reliability: Choose a calculator from a reputable source to ensure accuracy and avoid unreliable results.
Practical Applications of Rectangular Pyramid Volume Calculations
Calculating the volume of rectangular pyramids has widespread applications in various fields:
- Architecture and Construction: Determining the volume of pyramidal roofs, decorative elements, or structural components. Accurate volume calculations are essential for material estimation and cost planning.
- Engineering: Calculating the volume of pyramidal components in mechanical designs, civil engineering structures (like retaining walls), and other engineering applications.
- Mining and Geology: Estimating the volume of pyramidal ore deposits or rock formations. This is vital for resource management and extraction planning.
- Agriculture: Calculating the volume of pyramidal grain silos or other storage structures. Accurate volume assessment is crucial for inventory management.
- 3D Modeling and Game Development: Creating realistic and accurate 3D models requires precise volume calculations of various shapes, including rectangular pyramids. This is vital for realism in computer graphics and virtual environments.
- Mathematics and Education: The concept of rectangular pyramid volume calculation is a fundamental concept in geometry and is used for educational purposes at various levels.
Beyond the Basics: Variations and Considerations
While the basic formula covers most scenarios, there are some variations and considerations:
- Oblique Pyramids: The standard formula applies only to right rectangular pyramids where the apex is directly above the center of the rectangular base. For oblique pyramids (where the apex is not directly above the center), the calculation is more complex and may require advanced techniques or specialized software.
- Units of Measurement: Always ensure consistency in units of measurement. If the length, width, and height are given in different units (e.g., meters, centimeters), convert them to a single unit before applying the formula to avoid errors.
- Frustums: A truncated pyramid (a frustum) is a pyramid with its top portion removed. Calculating the volume of a frustum requires a different formula, taking into account the dimensions of both the top and bottom bases.
Troubleshooting and Error Handling
When using a rectangular pyramid volume calculator or performing manual calculations, common errors include:
- Incorrect Input: Double-check the values entered for length, width, and height to ensure accuracy.
- Unit Inconsistency: Ensure consistent units throughout the calculation.
- Formula Misapplication: Carefully review the formula and ensure it's applied correctly.
Conclusion: Mastering Rectangular Pyramid Volume Calculations
The ability to calculate the volume of a rectangular pyramid is a valuable skill with extensive practical applications. While manual calculations are feasible for simple problems, utilizing a reliable online calculator significantly enhances speed, accuracy, and efficiency. By understanding the formula, employing appropriate calculators, and considering potential variations, you can confidently tackle a wide range of rectangular pyramid volume calculations in various fields. Remember to always double-check your inputs and choose a reputable online calculator for the best results.
Latest Posts
Related Post
Thank you for visiting our website which covers about Volume Of A Rectangular Pyramid Calculator . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.