What Are All Factors Of 8
News Co
Apr 08, 2025 · 6 min read
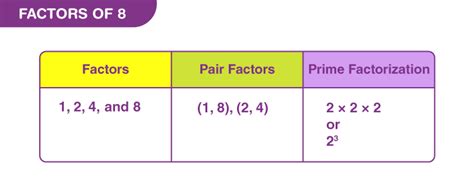
Table of Contents
What Are All the Factors of 8? A Deep Dive into Divisibility and Number Theory
The seemingly simple question, "What are all the factors of 8?" opens a door to a fascinating world of number theory, divisibility rules, and the fundamental building blocks of mathematics. While the immediate answer might seem straightforward, exploring this question fully allows us to delve into concepts that are crucial for understanding more complex mathematical ideas. This comprehensive guide will not only answer the question directly but also explore the broader mathematical context, providing you with a solid understanding of factors, divisors, and their significance.
Understanding Factors and Divisors
Before we tackle the factors of 8, let's establish a clear definition. A factor (or divisor) of a number is any integer that divides that number without leaving a remainder. In simpler terms, if you can divide a number by another number and get a whole number as the result, then the number you divided by is a factor.
For example, the factors of 12 are 1, 2, 3, 4, 6, and 12, because each of these numbers divides 12 evenly. Understanding factors is fundamental to many areas of mathematics, including algebra, number theory, and cryptography.
Finding the Factors of 8: A Step-by-Step Approach
Now, let's determine all the factors of 8. We'll approach this systematically to illustrate the process clearly:
-
Start with 1: Every positive integer has 1 as a factor.
-
Check for 2: 8 divided by 2 equals 4, so 2 is a factor.
-
Check for 3: 8 divided by 3 leaves a remainder, so 3 is not a factor.
-
Check for 4: 8 divided by 4 equals 2, so 4 is a factor.
-
Check for 5: 8 divided by 5 leaves a remainder, so 5 is not a factor.
-
Check for 6: 8 divided by 6 leaves a remainder, so 6 is not a factor.
-
Check for 7: 8 divided by 7 leaves a remainder, so 7 is not a factor.
-
Check for 8: 8 divided by 8 equals 1, so 8 is a factor.
Therefore, the factors of 8 are 1, 2, 4, and 8.
Visualizing Factors: The Factor Tree
A helpful tool for visualizing factors is the factor tree. While it's not strictly necessary for a small number like 8, it becomes incredibly useful for larger numbers. A factor tree breaks down a number into its prime factors. Let's illustrate this with 8:
8
/ \
2 4
/ \
2 2
This tree shows that 8 can be expressed as 2 x 2 x 2, or 2³. This prime factorization is unique to every number (Fundamental Theorem of Arithmetic) and provides a powerful way to find all factors.
From Factors to Prime Factorization: The Fundamental Theorem of Arithmetic
The prime factorization of 8 (2 x 2 x 2 or 2³) is crucial. The Fundamental Theorem of Arithmetic states that every integer greater than 1 can be uniquely represented as a product of prime numbers. This theorem underpins many number theory concepts. Understanding prime factorization helps us quickly identify all the factors of a number.
To find all factors of a number using its prime factorization, we consider all possible combinations of its prime factors. For example, with 8 (2³):
- 2⁰ = 1
- 2¹ = 2
- 2² = 4
- 2³ = 8
These combinations give us all the factors: 1, 2, 4, and 8.
Types of Factors: Exploring Different Classifications
Factors can be categorized in various ways:
-
Prime Factors: These are the prime numbers that multiply to give the original number. For 8, the only prime factor is 2.
-
Composite Factors: These are factors that are not prime numbers. For 8, the composite factors are 4 and 8.
-
Proper Factors: These are all factors excluding the number itself. For 8, the proper factors are 1, 2, and 4.
-
Greatest Common Factor (GCF): This is the largest factor common to two or more numbers.
-
Least Common Multiple (LCM): This is the smallest positive number that is a multiple of two or more numbers.
Understanding these classifications allows for more nuanced analysis of number relationships.
Applications of Factors: Real-World Examples
The concept of factors extends far beyond abstract mathematical exercises. It has practical applications in various fields:
-
Geometry: Calculating area and volume often involves factoring. For example, finding the dimensions of a rectangular box with a given volume.
-
Computer Science: Many algorithms in computer science rely on the properties of factors, prime numbers and factorization (e.g., cryptography, hashing).
-
Engineering: Designing structures and systems often involves factoring to determine optimal dimensions and configurations.
-
Music Theory: Understanding factors plays a role in music theory, particularly in understanding musical intervals and harmonies.
Beyond 8: Exploring Factors of Other Numbers
The principles discussed for finding the factors of 8 can be applied to any positive integer. Let's consider a few examples to solidify our understanding:
-
Factors of 12: 1, 2, 3, 4, 6, 12. Prime factorization: 2² x 3.
-
Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24. Prime factorization: 2³ x 3.
-
Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36. Prime factorization: 2² x 3².
Notice how the prime factorization helps in systematically identifying all factors. For larger numbers, the prime factorization method becomes increasingly efficient.
Advanced Concepts: Perfect Numbers and Abundant Numbers
Let's explore some fascinating number theory concepts related to factors:
-
Perfect Numbers: A perfect number is a positive integer that is equal to the sum of its proper divisors (excluding itself). 6 is a perfect number (1 + 2 + 3 = 6). Finding perfect numbers is an active area of research in number theory.
-
Abundant Numbers: An abundant number is a positive integer where the sum of its proper divisors is greater than the number itself. 12 is an abundant number (1 + 2 + 3 + 4 + 6 = 16 > 12).
-
Deficient Numbers: A deficient number is a positive integer where the sum of its proper divisors is less than the number itself. Most numbers are deficient.
Conclusion: The Significance of Factors in Mathematics and Beyond
The seemingly simple question of determining the factors of 8 has led us on a journey through fundamental concepts in number theory. From understanding basic divisibility to exploring prime factorization, perfect numbers, and abundant numbers, we’ve uncovered a rich mathematical landscape. The ability to find factors is not only a valuable skill for solving mathematical problems but also has applications in various fields, highlighting the interconnectedness of mathematics and the real world. Remember, the seemingly simple concepts often hold the key to unlocking more profound mathematical understanding.
Latest Posts
Latest Posts
-
Find The Least Common Multiple Of 4 And 7
Apr 08, 2025
-
Find The Inverse Of The Function Y 2x2 2
Apr 08, 2025
-
What Number Is A Multiple Of 3
Apr 08, 2025
-
Long Division Problems For 6th Graders
Apr 08, 2025
-
What Is A Prime Factorization Of 24
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about What Are All Factors Of 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.