What Are All Of The Factors Of 33
News Co
Apr 03, 2025 · 5 min read
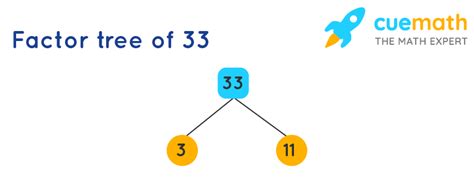
Table of Contents
What are all of the Factors of 33? A Deep Dive into Number Theory
The seemingly simple question, "What are all the factors of 33?" opens a door to a fascinating exploration of number theory, a branch of mathematics brimming with intriguing concepts and relationships. While the immediate answer might seem straightforward, delving deeper reveals the rich mathematical landscape surrounding factors, divisors, prime numbers, and their properties. This article will not only answer the question directly but also provide a comprehensive understanding of the concepts involved, enhancing your appreciation for the beauty and elegance of mathematics.
Understanding Factors and Divisors
Before we tackle the factors of 33, let's clarify the terminology. In mathematics, factors (or divisors) are numbers that divide another number without leaving a remainder. In simpler terms, if you can divide a number by another number evenly (resulting in a whole number), then the second number is a factor of the first.
For example, the factors of 12 are 1, 2, 3, 4, 6, and 12 because each of these numbers divides 12 without leaving a remainder. 12 ÷ 1 = 12, 12 ÷ 2 = 6, 12 ÷ 3 = 4, 12 ÷ 4 = 3, 12 ÷ 6 = 2, and 12 ÷ 12 = 1.
Finding the Factors of 33
Now, let's address the main question: what are the factors of 33? We need to find all the whole numbers that divide 33 without leaving a remainder.
Let's systematically explore:
- 1: 33 ÷ 1 = 33. 1 is always a factor of any number.
- 3: 33 ÷ 3 = 11. 3 is a factor of 33.
- 11: 33 ÷ 11 = 3. 11 is a factor of 33.
- 33: 33 ÷ 33 = 1. The number itself is always a factor.
Therefore, the factors of 33 are 1, 3, 11, and 33.
Prime Factorization and its Significance
The process of finding factors becomes particularly insightful when we consider prime factorization. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. Examples include 2, 3, 5, 7, 11, and so on. Prime factorization is the process of expressing a number as a product of its prime factors.
In the case of 33, its prime factorization is simply 3 x 11. Both 3 and 11 are prime numbers. This factorization is unique to 33; every composite number (a number that is not prime) has a unique prime factorization. This fundamental theorem of arithmetic is a cornerstone of number theory.
The prime factorization provides a powerful tool for finding all the factors of a number. To find all the factors of 33, we can consider all possible combinations of its prime factors:
- Using only 1: 1
- Using 3: 3
- Using 11: 11
- Using 3 and 11: 3 x 11 = 33
This method systematically generates all the factors of 33, reaffirming our earlier findings.
Beyond 33: Exploring Factorization Techniques
Understanding the factors of 33 provides a foundation for exploring factorization techniques applicable to larger numbers. While trial division (testing all numbers up to the square root of the number) is feasible for smaller numbers, it becomes inefficient for larger ones. More advanced methods include:
-
Sieve of Eratosthenes: An ancient algorithm for finding all prime numbers up to a specified integer. This helps in identifying potential prime factors.
-
Factorization Algorithms: Sophisticated algorithms, like the quadratic sieve and the general number field sieve, are used to factor extremely large numbers, crucial in cryptography. These algorithms are computationally intensive and often require specialized hardware.
The Significance of Factors in Mathematics and Beyond
The concept of factors extends far beyond simple arithmetic exercises. It plays a crucial role in various areas of mathematics and its applications:
-
Number Theory: Factors form the basis for understanding prime numbers, divisibility rules, and other fundamental concepts in number theory.
-
Algebra: Factoring polynomials (expressions with variables) is a key skill in algebra, enabling simplification and solving equations.
-
Cryptography: The difficulty of factoring large numbers into their prime factors underpins many modern encryption methods, ensuring secure online transactions and data protection.
-
Computer Science: Efficient algorithms for factorization are essential in computer science for various applications, including cryptography and data analysis.
Practical Applications and Real-World Examples
Factors have practical applications in numerous real-world scenarios:
-
Dividing Resources: Imagine dividing 33 items equally among groups. The factors of 33 (1, 3, 11, 33) represent the possible sizes of these groups.
-
Arranging Objects: If you have 33 tiles, you could arrange them in various rectangular grids whose dimensions are pairs of factors of 33 (1x33, 3x11).
-
Scheduling: If a task takes 33 hours, the factors help determine possible work schedules (e.g., 3 hours/day for 11 days or 11 hours/day for 3 days).
-
Geometry: Factors play a role in determining the dimensions of geometric shapes based on area or volume considerations.
Conclusion: The Richness of Number Theory
The seemingly simple question of finding the factors of 33 has led us on a journey into the fascinating world of number theory. We discovered that the factors of 33 are 1, 3, 11, and 33, and explored the concept of prime factorization, which is a fundamental tool in understanding the structure of numbers. This exploration highlights the power and elegance of mathematics and its far-reaching applications in various fields, demonstrating how even seemingly basic concepts can hold profound mathematical significance. The study of factors and divisors serves as a compelling entry point into the intricate and rewarding world of mathematical exploration.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Are All Of The Factors Of 33 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.