What Are All The Factors For 50
News Co
Apr 03, 2025 · 5 min read
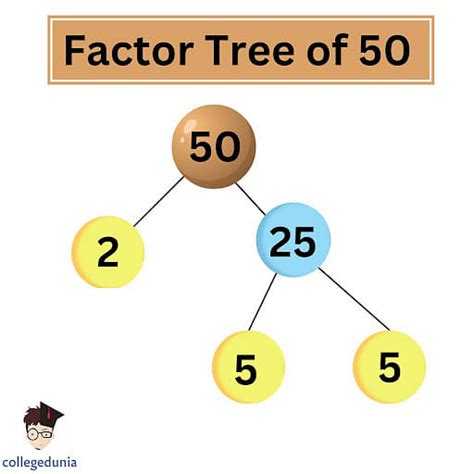
Table of Contents
Decomposing 50: A Deep Dive into its Factors and Properties
The seemingly simple number 50 hides a wealth of mathematical richness. Understanding its factors, prime factorization, divisors, and related properties offers a fascinating glimpse into number theory. This exploration goes beyond a simple list; we'll delve into the concepts, applications, and connections to other mathematical areas.
What are Factors?
Before we dissect 50, let's define our key term: factors. Factors of a number are whole numbers that divide evenly into that number without leaving a remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12 because each of these numbers divides 12 without leaving a remainder.
Finding the Factors of 50
To find the factors of 50, we systematically check each whole number to see if it divides 50 evenly. We can start with 1 and work our way up:
- 1: 50 ÷ 1 = 50 (1 is always a factor)
- 2: 50 ÷ 2 = 25
- 5: 50 ÷ 5 = 10
- 10: 50 ÷ 10 = 5
- 25: 50 ÷ 25 = 2
- 50: 50 ÷ 50 = 1 (the number itself is always a factor)
Therefore, the factors of 50 are 1, 2, 5, 10, 25, and 50. Notice that the factors appear in pairs, except for the number itself when it's a perfect square (as 50 is not, it doesn't have this property, in this case).
Prime Factorization of 50
Prime factorization is expressing a number as the product of its prime factors. Prime numbers are whole numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11...). To find the prime factorization of 50, we repeatedly divide by prime numbers until we're left with only prime numbers:
50 = 2 × 25 = 2 × 5 × 5
Therefore, the prime factorization of 50 is 2 × 5<sup>2</sup>. This representation is unique to every number (Fundamental Theorem of Arithmetic).
Divisors vs. Factors: A Clarification
The terms "factors" and "divisors" are often used interchangeably, and in the context of 50, they mean the same thing: the numbers that divide 50 evenly. However, a subtle difference emerges when discussing more complex concepts in number theory. While factors generally refer to the numbers that divide a number, divisors can be used more broadly to include concepts like common divisors and greatest common divisors (GCD). For our purposes concerning 50, they're equivalent.
Properties Related to Factors of 50
Let's explore some properties linked to the factors of 50:
-
Sum of Factors: Adding up all the factors of 50 (1 + 2 + 5 + 10 + 25 + 50) gives us 93. This sum has its own significance in number theory.
-
Number of Factors: 50 has a total of six factors. The number of factors can be determined directly from the prime factorization. In the case of 50 (2¹ × 5²), the number of factors is calculated as (1+1)(2+1) = 6. This formula works for any number given its prime factorization.
-
Even and Odd Factors: 50 has both even (2, 10, 50) and odd (1, 5, 25) factors. This is because its prime factorization includes both an even prime (2) and an odd prime (5).
-
Perfect Number Relationship: A perfect number is a positive integer that is equal to the sum of its proper divisors (divisors excluding the number itself). 50 is not a perfect number; the sum of its proper divisors (1 + 2 + 5 + 10 + 25 = 43) is not equal to 50.
Applications of Understanding Factors
Understanding the factors of a number like 50 has various practical applications:
-
Divisibility Rules: Knowing the factors helps determine divisibility. For example, since 2 and 5 are factors of 50, 50 is divisible by both 2 and 5.
-
Fraction Simplification: When simplifying fractions, finding common factors between the numerator and denominator is crucial. If you had the fraction 50/100, knowing that 50 is a factor of 100 allows you to simplify it to 1/2.
-
Algebraic Factoring: In algebra, factoring expressions often involves finding common factors. This skill is fundamental for solving equations and simplifying expressions.
-
Combinatorics and Number Theory: The properties of factors, such as the number of factors and the sum of factors, have applications in various areas of mathematics, particularly combinatorics and number theory.
50 in Different Contexts
The number 50 transcends its purely mathematical significance. It appears in various contexts:
-
Measurement: 50 represents a significant halfway point in many measurement systems (e.g., 50 centimeters is half a meter).
-
Sports and Games: In many sports, 50 holds symbolic importance (e.g., 50-yard line in American football).
-
Everyday Life: We encounter the number 50 frequently in everyday situations (e.g., 50 years old, 50 cents).
Exploring Beyond 50: Extending the Concepts
The analysis of 50's factors provides a foundation for exploring more complex number-theoretic concepts:
-
Greatest Common Divisor (GCD): Finding the GCD of two or more numbers involves identifying the largest number that divides all of them evenly.
-
Least Common Multiple (LCM): The LCM is the smallest number that is a multiple of all the given numbers.
-
Modular Arithmetic: This branch of number theory deals with remainders after division, which is directly related to factors.
Conclusion: The Richness of a Simple Number
While 50 may seem like a simple number at first glance, a closer examination reveals a fascinating array of properties and applications. Understanding its factors, prime factorization, and related concepts provides valuable insights into number theory and its practical implications. This exploration extends beyond a mere calculation; it highlights the interconnectedness of mathematical ideas and their relevance to various aspects of our world. From simplifying fractions to solving algebraic equations, the principles we've explored using 50 as an example are fundamental building blocks for more advanced mathematical concepts. The seemingly straightforward number 50 serves as a compelling demonstration of the depth and beauty hidden within the world of numbers.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Are All The Factors For 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.