What Are All The Factors Of 99
News Co
Apr 05, 2025 · 5 min read
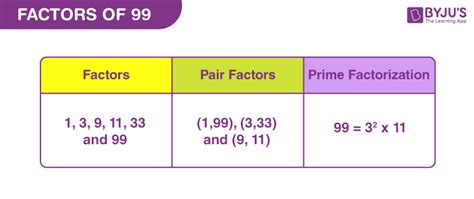
Table of Contents
What Are All the Factors of 99? A Deep Dive into Number Theory
Finding all the factors of a number might seem like a simple mathematical task, but understanding the process reveals fundamental concepts in number theory. This article delves into the factors of 99, exploring various methods to identify them and connecting this seemingly basic exercise to broader mathematical principles. We'll also touch upon the applications of factor finding in more complex scenarios.
Understanding Factors and Divisibility
Before we pinpoint the factors of 99, let's define what a factor is. A factor (or divisor) of a number is any integer that divides the number exactly, leaving no remainder. In other words, if 'a' is a factor of 'b', then b/a is a whole number.
Divisibility rules can often speed up the process of finding factors. For 99, we can immediately apply some basic rules:
- Divisibility by 1: Every number is divisible by 1, so 1 is a factor of 99.
- Divisibility by 3: The sum of the digits of 99 (9 + 9 = 18) is divisible by 3, therefore 99 is divisible by 3.
- Divisibility by 9: The sum of the digits (18) is also divisible by 9, so 99 is divisible by 9.
- Divisibility by 11: 99 divided by 11 is 9, with no remainder.
Systematic Factor Finding for 99
Now let's systematically determine all the factors. One efficient method is to check for divisors starting from 1 and working our way up to the square root of the number. The square root of 99 is approximately 9.95. We only need to check integers up to 9. Any factor larger than 9 will have a corresponding factor smaller than 9. This is because factors always come in pairs (except for perfect squares, where the square root is a factor paired with itself).
Let's test the integers:
- 1: 99 / 1 = 99
- 3: 99 / 3 = 33
- 9: 99 / 9 = 11
We've found three pairs of factors: (1, 99), (3, 33), and (9, 11). Since we've checked up to 9 (approximately the square root of 99), we've found all the factors.
The Complete List of Factors of 99
Therefore, the complete list of factors of 99 is: 1, 3, 9, 11, 33, and 99.
Prime Factorization and its Relation to Factors
Understanding prime factorization is crucial for finding all factors of any number. Prime factorization is the process of expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves).
The prime factorization of 99 is 3 x 3 x 11, or 3² x 11.
From the prime factorization, we can easily derive all the factors. We systematically combine the prime factors:
- Using only 3: 3¹ = 3
- Using only 11: 11¹ = 11
- Combining 3 and 11: 3¹ x 11¹ = 33
- Combining two 3s and 11: 3² x 11¹ = 99
- Using only 1 (implicitly present in the prime factorization): 1
This method confirms our earlier list: 1, 3, 9, 11, 33, and 99. Prime factorization provides a structured and reliable way to find all factors, especially for larger numbers.
Applications of Factor Finding
The seemingly simple task of finding factors has significant applications across various fields:
1. Cryptography
Factorization plays a vital role in modern cryptography, particularly in RSA encryption. RSA relies on the difficulty of factoring large numbers, specifically the product of two large prime numbers. The security of many online transactions depends on this computational challenge.
2. Computer Science
In computer science, algorithms for finding factors are crucial for tasks like optimizing code, managing memory allocation, and developing efficient data structures. Understanding factors contributes to the development of faster and more efficient algorithms.
3. Number Theory Research
Factorization is a cornerstone of number theory research. Many unsolved problems in number theory, such as the Riemann Hypothesis, are intimately connected to the properties of prime numbers and factorization. Understanding factor patterns reveals insights into the deeper structure of numbers.
4. Mathematics Education
Finding factors provides a fundamental introduction to concepts like divisibility, prime numbers, and number theory. It helps build a solid foundation for more advanced mathematical studies.
Beyond 99: Exploring Factorization Techniques for Larger Numbers
For larger numbers, finding factors manually becomes increasingly tedious. More sophisticated algorithms are necessary. Some common techniques include:
- Trial Division: Systematically dividing the number by all integers up to its square root.
- Sieve of Eratosthenes: Efficiently generating a list of prime numbers, which are then used to check for prime factors.
- Pollard's Rho Algorithm: A probabilistic algorithm commonly used for factoring large numbers.
- General Number Field Sieve (GNFS): The most efficient known algorithm for factoring extremely large numbers.
These algorithms are essential for tackling factorization challenges in cryptography and number theory research.
Conclusion: The Significance of Factors in Mathematics and Beyond
While finding the factors of 99 might seem like a straightforward exercise, it reveals the underlying principles of number theory and highlights the importance of factorization in various fields. From cryptography to computer science and number theory research, the ability to effectively find and analyze factors is crucial for solving complex problems and driving advancements in technology and mathematics. This seemingly simple concept has far-reaching implications and offers a fascinating window into the intricate world of numbers. The seemingly simple task of finding the factors of 99 serves as a valuable stepping stone towards a deeper understanding of the mathematical world.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Are All The Factors Of 99 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.