What Are The Common Factors Of 15 And 20
News Co
Apr 04, 2025 · 5 min read
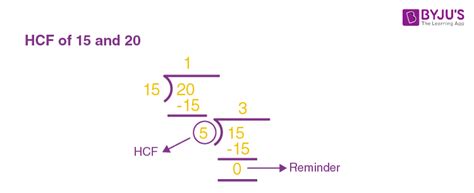
Table of Contents
What are the Common Factors of 15 and 20? A Deep Dive into Number Theory
Finding the common factors of two numbers might seem like a simple task, especially with smaller numbers like 15 and 20. However, understanding the underlying principles reveals a fascinating glimpse into number theory, a branch of mathematics with applications far beyond basic arithmetic. This article explores not only the common factors of 15 and 20 but also delves into the broader concepts of factors, prime factorization, greatest common factor (GCF), and their significance in mathematics and beyond.
Understanding Factors
Before we tackle the specific problem of finding the common factors of 15 and 20, let's establish a solid understanding of what a factor is. A factor of a number is any whole number that divides evenly into that number without leaving a remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12, because each of these numbers divides 12 without any remainder.
Identifying Factors of 15
Let's find the factors of 15. We can systematically check each whole number:
- 1 divides 15 (15 ÷ 1 = 15)
- 3 divides 15 (15 ÷ 3 = 5)
- 5 divides 15 (15 ÷ 5 = 3)
- 15 divides 15 (15 ÷ 15 = 1)
Therefore, the factors of 15 are 1, 3, 5, and 15.
Identifying Factors of 20
Now, let's identify the factors of 20:
- 1 divides 20 (20 ÷ 1 = 20)
- 2 divides 20 (20 ÷ 2 = 10)
- 4 divides 20 (20 ÷ 4 = 5)
- 5 divides 20 (20 ÷ 5 = 4)
- 10 divides 20 (20 ÷ 10 = 2)
- 20 divides 20 (20 ÷ 20 = 1)
Therefore, the factors of 20 are 1, 2, 4, 5, 10, and 20.
Finding the Common Factors
Now that we have listed all the factors of 15 and 20, we can easily identify the common factors. These are the numbers that appear in both lists:
The common factors of 15 and 20 are 1 and 5.
Prime Factorization: A Deeper Look
Understanding prime factorization provides a more efficient method for finding the common factors of larger numbers. A prime number is a whole number greater than 1 that has only two factors: 1 and itself. Prime factorization is the process of expressing a number as a product of its prime factors.
Prime Factorization of 15
15 can be expressed as 3 x 5. Both 3 and 5 are prime numbers. Therefore, the prime factorization of 15 is 3 x 5.
Prime Factorization of 20
20 can be expressed as 2 x 2 x 5, or 2² x 5. Both 2 and 5 are prime numbers. Therefore, the prime factorization of 20 is 2² x 5.
Using Prime Factorization to Find Common Factors
By comparing the prime factorizations of 15 and 20, we can easily identify the common factors. Both numbers share the prime factor 5. This means that 5 is a common factor. Since 1 is a factor of every number, 1 is also a common factor. Therefore, the common factors are 1 and 5, confirming our previous result.
Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the highest common factor (HCF), is the largest number that divides evenly into two or more numbers. In our case, the GCF of 15 and 20 is 5. This is the largest number that is a factor of both 15 and 20.
Applications of GCF and Common Factors
The concepts of GCF and common factors are not just abstract mathematical ideas; they have numerous practical applications:
-
Simplifying Fractions: Finding the GCF is crucial for simplifying fractions to their lowest terms. For example, the fraction 15/20 can be simplified by dividing both the numerator and denominator by their GCF (5), resulting in the equivalent fraction 3/4.
-
Measurement and Division: When dividing objects or quantities into equal groups, the GCF helps determine the largest possible group size. For example, if you have 15 apples and 20 oranges, you can divide them into groups of 5, each group containing 3 apples and 4 oranges.
-
Geometry and Area: GCF plays a role in solving geometric problems related to area and dimensions. For example, when finding the dimensions of the largest square tile that can be used to cover a rectangular floor of 15 units by 20 units, the GCF (5) is the side length of the largest square tile.
-
Algebra and Equation Solving: GCF is frequently used in algebraic manipulations, such as factoring polynomials.
-
Computer Science: GCF algorithms are essential in various areas of computer science, including cryptography and data compression.
Beyond 15 and 20: Extending the Concepts
The principles discussed above extend to finding common factors and GCF of any two or more numbers. The method of prime factorization remains a powerful tool, especially for larger numbers. For example, let's find the common factors of 24 and 36:
- Prime Factorization of 24: 2³ x 3
- Prime Factorization of 36: 2² x 3²
Comparing the prime factorizations, we see that both numbers share 2² and 3. Therefore, the common factors are 1, 2, 3, 4, 6, and 12. The GCF is 12.
Euclidean Algorithm: An Efficient Method
For larger numbers, the Euclidean algorithm provides a more efficient way to find the GCF. This algorithm is based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF. This algorithm is particularly useful for numbers that are too large for easy prime factorization.
Conclusion
Finding the common factors of 15 and 20, while seemingly straightforward, opens the door to a deeper understanding of fundamental mathematical concepts. Understanding factors, prime factorization, and the greatest common factor is crucial not only for solving basic mathematical problems but also for tackling more complex problems in various fields. The methods described in this article, including prime factorization and the Euclidean algorithm, provide practical and efficient tools for finding common factors and GCFs, expanding our ability to solve mathematical challenges and appreciate the beauty and utility of number theory. From simplifying fractions to solving geometric problems and beyond, the application of these concepts is widespread and vital in numerous disciplines.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Are The Common Factors Of 15 And 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.