What Are The Common Factors Of 24 And 32
News Co
Apr 04, 2025 · 5 min read
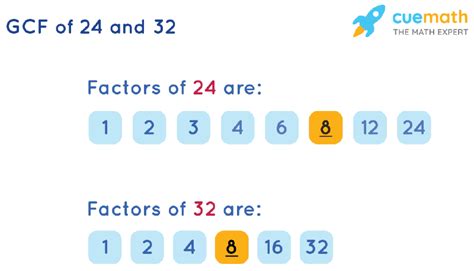
Table of Contents
Unveiling the Common Factors of 24 and 32: A Deep Dive into Number Theory
Finding the common factors of two numbers might seem like a simple arithmetic task, but it opens a door to a fascinating world of number theory, with implications reaching far beyond basic calculations. This article delves deep into determining the common factors of 24 and 32, exploring various methods, explaining the underlying mathematical principles, and showcasing the broader significance of this seemingly straightforward concept.
Understanding Factors and Common Factors
Before we embark on our journey to find the common factors of 24 and 32, let's solidify our understanding of some key terms:
-
Factors: Factors of a number are whole numbers that divide the number evenly without leaving a remainder. For instance, the factors of 12 are 1, 2, 3, 4, 6, and 12.
-
Common Factors: Common factors are numbers that are factors of two or more numbers. These are the numbers that divide both numbers evenly.
Our mission is to identify the common factors shared by 24 and 32.
Method 1: Listing Factors
The most straightforward approach is to list all the factors of each number and then identify the numbers that appear in both lists.
Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
Factors of 32: 1, 2, 4, 8, 16, 32
Comparing the two lists, we find that the common factors of 24 and 32 are 1, 2, 4, and 8.
Method 2: Prime Factorization
A more sophisticated and efficient method involves prime factorization. Prime factorization breaks a number down into its prime components – numbers divisible only by 1 and themselves.
Prime Factorization of 24:
24 = 2 x 2 x 2 x 3 = 2³ x 3
Prime Factorization of 32:
32 = 2 x 2 x 2 x 2 x 2 = 2⁵
To find the common factors, we identify the prime factors that both numbers share and their lowest common power. Both 24 and 32 share the prime factor 2. The lowest power of 2 present in both factorizations is 2³.
Therefore, the common factors are:
- 2⁰ = 1
- 2¹ = 2
- 2² = 4
- 2³ = 8
This method confirms that the common factors of 24 and 32 are 1, 2, 4, and 8.
Method 3: Greatest Common Divisor (GCD)
The greatest common divisor (GCD), also known as the highest common factor (HCF), is the largest number that divides both numbers without leaving a remainder. Finding the GCD provides a shortcut to finding all common factors.
Several methods exist to calculate the GCD:
- Euclidean Algorithm: This is an efficient algorithm for finding the GCD of two numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD.
Let's apply the Euclidean algorithm to 24 and 32:
- 32 ÷ 24 = 1 with a remainder of 8
- 24 ÷ 8 = 3 with a remainder of 0
The last non-zero remainder is 8, so the GCD of 24 and 32 is 8.
Once we know the GCD, we know that all factors of the GCD are also common factors of the original numbers. The factors of 8 are 1, 2, 4, and 8. Therefore, the common factors are 1, 2, 4, and 8.
- Prime Factorization Method (for GCD): Using the prime factorizations from Method 2, we identify the common prime factors and their lowest powers. In this case, the common prime factor is 2, and the lowest power is 2³. Therefore, the GCD is 2³ = 8.
The Significance of Common Factors
The concept of common factors extends far beyond simple arithmetic exercises. It has profound implications in various mathematical fields and real-world applications:
-
Fraction Simplification: Finding the GCD is crucial for simplifying fractions. To simplify a fraction, we divide both the numerator and the denominator by their GCD.
-
Algebra: GCD is used in simplifying algebraic expressions and solving equations.
-
Number Theory: The study of common factors is fundamental to understanding concepts like prime numbers, relatively prime numbers (numbers with a GCD of 1), and modular arithmetic.
-
Computer Science: Algorithms for finding GCD are essential in cryptography and other computational areas. Efficient GCD algorithms are vital for optimizing performance.
-
Real-world Applications: Common factors are applied in various practical situations, including:
- Dividing objects equally: Determining the maximum number of equal groups that can be formed from a set of objects.
- Scheduling: Finding common time intervals for meetings or events.
- Geometry: Calculations involving lengths, areas, and volumes often require finding common factors.
Exploring Further: Least Common Multiple (LCM)
While we've focused on common factors, it's worth briefly mentioning the least common multiple (LCM). The LCM is the smallest number that is a multiple of two or more numbers. The relationship between GCD and LCM is expressed by the formula:
GCD(a, b) x LCM(a, b) = a x b
For 24 and 32:
GCD(24, 32) = 8
LCM(24, 32) = (24 x 32) / 8 = 96
This formula highlights the interconnectedness of GCD and LCM, both essential concepts in number theory.
Conclusion: Beyond the Basics
Finding the common factors of 24 and 32, while seemingly a basic arithmetic task, reveals the rich tapestry of number theory. By employing various methods, from simple listing to the sophisticated Euclidean algorithm, we've uncovered the common factors: 1, 2, 4, and 8. Understanding these concepts lays a solid foundation for further exploration of number theory and its numerous applications across diverse fields. The seemingly simple act of finding common factors unlocks a deeper appreciation for the elegant structures and fundamental principles governing numbers. It's a testament to the power of mathematics to illuminate seemingly simple concepts and their surprising depth. This exploration encourages a deeper understanding not only of the specific problem but also of the broader mathematical landscape it inhabits. Remember that consistent practice and exploration are key to mastering these fundamental concepts and unlocking the fascinating world of number theory.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Are The Common Factors Of 24 And 32 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.