What Are The Differences Between A Square And A Rhombus
News Co
Apr 07, 2025 · 5 min read
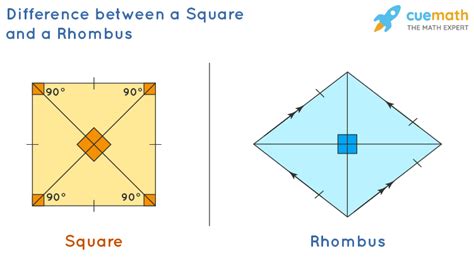
Table of Contents
What are the Differences Between a Square and a Rhombus? A Deep Dive into Quadrilaterals
Squares and rhombuses are both quadrilaterals, meaning they are two-dimensional shapes with four sides. However, despite their similarities, there are key distinctions that set them apart. Understanding these differences is crucial for anyone studying geometry, whether at a basic or advanced level. This article will delve into the characteristics of both shapes, highlighting their similarities and, more importantly, their crucial differences. We'll explore their properties, angles, diagonals, and area calculations to provide a comprehensive understanding of these fundamental geometric figures.
Similarities: The Common Ground of Squares and Rhombuses
Before diving into their differences, let's acknowledge what squares and rhombuses do have in common:
- Four Sides: Both shapes possess four sides. This is the most fundamental similarity, placing them both firmly within the quadrilateral family.
- Closed Shape: Both are closed shapes, meaning all their sides connect to form a complete figure. There are no open ends or gaps.
- Straight Sides: Each side of both a square and a rhombus is a straight line segment. This differentiates them from shapes with curved sides.
While these commonalities are important, they are not sufficient to define either shape uniquely. The crucial distinctions lie in the specifics of their sides and angles.
Key Differences: Where Squares and Rhombuses Diverge
The significant differences between a square and a rhombus relate to their sides, angles, and consequently, their diagonals.
Side Lengths: The Defining Difference
This is arguably the most significant distinction:
- Square: A square possesses four sides of equal length. This is a defining characteristic.
- Rhombus: A rhombus also has four sides of equal length, just like a square.
While this might seem to blur the lines, remember that equal side length is a necessary but not sufficient condition to define a square. Other properties are required.
Angles: Right Angles vs. Variable Angles
This is where the crucial difference emerges:
- Square: A square has four right angles, meaning each angle measures 90 degrees. This is a fundamental property that distinguishes it from all other quadrilaterals except for rectangles.
- Rhombus: A rhombus can have any angle measure, provided opposite angles are equal and adjacent angles are supplementary (adding up to 180 degrees). This means a rhombus can have angles that are acute (less than 90 degrees), right (90 degrees), or obtuse (greater than 90 degrees). Only when all angles are 90 degrees does a rhombus become a special case – a square.
In essence: All squares are rhombuses (because they have four equal sides), but not all rhombuses are squares (because they don't necessarily have 90-degree angles). This highlights the hierarchical relationship between the two shapes.
Diagonals: A Further Distinguishing Feature
The diagonals of these shapes offer additional insight into their differences:
- Square: The diagonals of a square are equal in length, bisect each other at right angles, and bisect the angles of the square. This means each diagonal cuts the square into two congruent right-angled isosceles triangles.
- Rhombus: The diagonals of a rhombus are not necessarily equal in length, but they always bisect each other at right angles. They also bisect the angles of the rhombus. However, unlike in a square, the triangles formed by the diagonals are not necessarily isosceles.
The differing lengths of diagonals further emphasize that a rhombus is a more general shape than a square.
Visual Representations: Illustrating the Differences
Imagine drawing both shapes:
A square will look like a perfect, symmetrical box with all sides equal and all angles 90 degrees.
A rhombus, on the other hand, can appear as a tilted square, a diamond shape, or something in between. The key is that all four sides remain equal, but the angles can vary.
Area Calculation: A Comparative Approach
Calculating the area for both shapes uses slightly different formulas, although one can be derived from the other:
- Square: Area = side * side = side² (since all sides are equal)
- Rhombus: Area = base * height or Area = (1/2) * d1 * d2 (where d1 and d2 are the lengths of the diagonals). The second formula highlights the perpendicular bisecting property of the diagonals.
The simplicity of the square's area formula reflects its symmetrical nature. The rhombus's formula reflects its greater variability in shape.
Practical Applications: Squares and Rhombuses in the Real World
Both squares and rhombuses appear in various real-world applications:
-
Squares: We encounter squares frequently in architecture (building foundations, tiles), games (chessboards), and everyday objects (window panes, boxes). The stability and symmetry of squares make them ideal for construction and design.
-
Rhombuses: Rhombuses are less common in everyday objects, but their unique properties are exploited in certain applications. For example, the structure of some crystals is based on rhombus shapes. Furthermore, certain engineering applications leverage the unique diagonal properties of rhombuses for structural integrity. The design of certain mechanical components might utilize rhombus shapes for their efficient force distribution.
Conclusion: A Clear Distinction Between Two Quadrilaterals
While squares and rhombuses share some similarities as quadrilaterals with four sides, their key differences lie in their angles and the resulting properties of their diagonals. A square is a special case of a rhombus, possessing all the characteristics of a rhombus plus the additional property of having four right angles. This hierarchical relationship is fundamental to understanding the geometry of these shapes. By understanding these distinctions, one can better appreciate the unique characteristics and applications of both squares and rhombuses in various fields, from mathematics and geometry to engineering and design. Mastering the differences strengthens geometric understanding and problem-solving abilities. The differences in their properties lead to different applications and problem-solving approaches, making a clear understanding crucial for various disciplines.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Are The Differences Between A Square And A Rhombus . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.