What Are The Factors For 77
News Co
Apr 07, 2025 · 6 min read
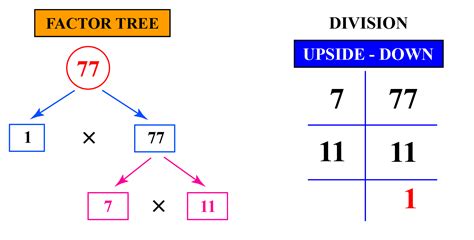
Table of Contents
Decoding the Enigma: Exploring the Factors of 77
The seemingly simple question, "What are the factors of 77?" opens a door to a deeper understanding of number theory, prime factorization, and the building blocks of mathematics. While the immediate answer might seem straightforward, delving into the subject reveals fascinating connections to more complex mathematical concepts. This article will not only answer the question directly but also explore the broader context of factors, prime numbers, and their significance in various mathematical fields.
Understanding Factors: The Building Blocks of Numbers
Before we tackle the specific case of 77, let's establish a firm understanding of what factors are. In simple terms, a factor of a number is any whole number that divides evenly into that number without leaving a remainder. For instance, the factors of 12 are 1, 2, 3, 4, 6, and 12, because each of these numbers divides 12 without leaving any remainder. Finding the factors of a number is essentially breaking it down into its multiplicative components.
This concept is fundamental in various branches of mathematics, including arithmetic, algebra, and number theory. Understanding factors is crucial for simplifying expressions, solving equations, and exploring the properties of numbers. It's the foundation upon which more advanced mathematical concepts are built.
Finding the Factors of 77: A Step-by-Step Approach
Now, let's focus on the number 77. To find its factors, we systematically check each whole number to see if it divides 77 without leaving a remainder. We can start with 1, which is a factor of every number.
- 1: 77 divided by 1 is 77, leaving no remainder. Therefore, 1 is a factor.
- 7: 77 divided by 7 is 11, leaving no remainder. Therefore, 7 is a factor.
- 11: 77 divided by 11 is 7, leaving no remainder. Therefore, 11 is a factor.
- 77: 77 divided by 77 is 1, leaving no remainder. Therefore, 77 itself is a factor.
We have now identified all the factors of 77: 1, 7, 11, and 77. There are no other whole numbers that divide 77 evenly.
The Significance of Prime Numbers and Prime Factorization
The factors of 77 – 7 and 11 – are both prime numbers. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. Prime numbers are the fundamental building blocks of all other whole numbers, much like atoms are the building blocks of matter. Every whole number greater than 1 can be expressed as a unique product of prime numbers. This is known as the Fundamental Theorem of Arithmetic.
The process of expressing a number as a product of its prime factors is called prime factorization. For 77, the prime factorization is simply 7 x 11. This is a unique representation; no other combination of prime numbers will multiply to give 77.
The prime factorization of a number is extremely useful in various mathematical operations, including:
- Simplifying fractions: Finding the greatest common divisor (GCD) of the numerator and denominator, which involves prime factorization, allows for significant simplification of fractions.
- Solving equations: Prime factorization can aid in solving certain types of equations, particularly those involving divisibility.
- Cryptography: Prime numbers play a crucial role in modern cryptography, underpinning many secure communication systems. The difficulty of factoring large numbers into their prime components forms the basis of the security of these systems.
Extending the Concept: Factors and Divisibility Rules
Understanding factors is intrinsically linked to divisibility rules. Divisibility rules are shortcuts to determine if a number is divisible by another number without performing the actual division. For example:
- Divisibility by 2: A number is divisible by 2 if its last digit is even (0, 2, 4, 6, or 8).
- Divisibility by 3: A number is divisible by 3 if the sum of its digits is divisible by 3.
- Divisibility by 5: A number is divisible by 5 if its last digit is 0 or 5.
- Divisibility by 11: A number is divisible by 11 if the alternating sum of its digits is divisible by 11. (e.g., 209: 2 - 0 + 9 = 11, which is divisible by 11, so 209 is divisible by 11).
These rules are helpful in quickly identifying some factors of a number, particularly for larger numbers. While they don't provide the complete set of factors, they offer a valuable starting point. In the case of 77, we can quickly see that it's not divisible by 2 or 5, but the divisibility rule for 11 would quickly help identify 11 as a factor.
Factors in Algebra and Beyond
The concept of factors extends far beyond basic arithmetic. In algebra, factoring is a crucial technique used to simplify expressions, solve equations, and analyze functions. Factoring quadratic expressions, for example, involves finding two expressions that multiply to give the original quadratic. This allows for solving quadratic equations and understanding the behavior of parabolic functions.
Furthermore, the concept of factors plays a vital role in advanced mathematical fields like number theory, abstract algebra, and even cryptography. The exploration of prime numbers and their properties is a significant area of research in number theory, with implications for other areas of mathematics and computer science.
Practical Applications of Understanding Factors
Beyond the theoretical realm, understanding factors has numerous practical applications:
- Data analysis: Factors are used in data analysis to identify patterns and relationships within datasets. For instance, in market research, understanding the factors that influence consumer behavior is critical.
- Engineering and design: Factors are used in engineering and design to determine the optimal dimensions and proportions for various structures and components.
- Computer science: Factors are crucial in algorithms and data structures, particularly those involving efficient searching and sorting.
- Music theory: Mathematical relationships, including factors, are often found in musical scales and harmonies.
The applications are extensive and diverse, highlighting the fundamental importance of understanding this core mathematical concept.
Conclusion: The Enduring Significance of Factors
The seemingly simple question about the factors of 77 has led us on a journey through various mathematical concepts. We've explored the definition of factors, the significance of prime numbers and prime factorization, the utility of divisibility rules, and the broader applications of factors in various fields.
Understanding factors is not merely an exercise in arithmetic; it's a key to unlocking deeper insights into the structure and properties of numbers, providing a foundation for more advanced mathematical exploration. The exploration of 77 and its factors serves as a microcosm of the elegance and power inherent within the study of mathematics. The simplicity of the initial problem belies the richness and depth of the concepts it connects to, underscoring the enduring significance of this fundamental mathematical idea. From basic arithmetic to advanced cryptography, the influence of factors is undeniable, making it a vital concept for anyone seeking a deeper understanding of the mathematical world.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Are The Factors For 77 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.