What Are The Factors For 88
News Co
Apr 05, 2025 · 6 min read
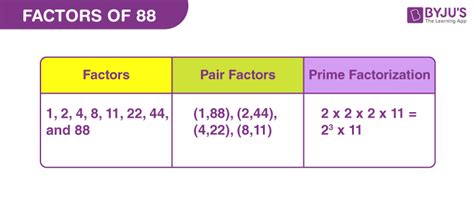
Table of Contents
Decoding the Enigma of "Factors for 88": A Deep Dive into Number Theory and Beyond
The seemingly simple question, "What are the factors of 88?", opens a door to a fascinating world of number theory, prime factorization, and even unexpected connections to other areas of mathematics and beyond. While the immediate answer might seem straightforward, exploring the concept of factors in detail reveals a rich tapestry of mathematical relationships and applications.
This article will delve deep into understanding the factors of 88, exploring the fundamental concepts, revealing advanced techniques, and uncovering the broader implications of this seemingly simple numerical inquiry.
Understanding Factors: The Building Blocks of Numbers
Before we tackle the specific factors of 88, let's establish a clear understanding of what a factor actually is. In simple terms, a factor of a number is any integer that divides that number without leaving a remainder. Alternatively, we can say that a factor is a number that can be multiplied by another integer to produce the original number.
For example, the factors of 12 are 1, 2, 3, 4, 6, and 12, because each of these numbers divides 12 evenly. This is because:
- 1 x 12 = 12
- 2 x 6 = 12
- 3 x 4 = 12
This simple definition lays the foundation for understanding the factors of any number, including 88.
Finding the Factors of 88: A Step-by-Step Approach
To find the factors of 88, we can use a systematic approach:
-
Start with 1 and the number itself: Every number is divisible by 1 and itself. Therefore, 1 and 88 are factors of 88.
-
Check for divisibility by small prime numbers: Prime numbers (numbers divisible only by 1 and themselves) are the building blocks of all other numbers. Let's check divisibility by 2, 3, 5, 7, and so on.
-
Divisibility by 2: 88 is an even number, so it's divisible by 2. 88 / 2 = 44. Therefore, 2 and 44 are factors.
-
Divisibility by 3: The sum of the digits of 88 (8 + 8 = 16) is not divisible by 3, so 88 is not divisible by 3.
-
Divisibility by 4: 88 is divisible by 4 because the last two digits (88) are divisible by 4. 88 / 4 = 22. Therefore, 4 and 22 are factors.
-
Divisibility by 5: 88 does not end in 0 or 5, so it's not divisible by 5.
-
Divisibility by 7: 88 divided by 7 leaves a remainder, so 7 is not a factor.
-
Divisibility by 8: 88 is divisible by 8 because 8 x 11 = 88. Therefore, 8 and 11 are factors.
-
-
Continue checking until the factors start to repeat: As we continue checking, we'll notice that the factors will start to repeat. Once we reach a factor whose square is greater than 88, we can stop.
Therefore, the complete list of factors for 88 is: 1, 2, 4, 8, 11, 22, 44, and 88.
Prime Factorization: The Fundamental Theorem of Arithmetic
A more powerful and elegant approach to finding factors involves prime factorization. The Fundamental Theorem of Arithmetic states that every integer greater than 1 can be represented uniquely as a product of prime numbers. This unique representation is known as the prime factorization of the number.
Let's find the prime factorization of 88:
- 88 is an even number, so it's divisible by 2: 88 = 2 x 44
- 44 is also divisible by 2: 44 = 2 x 22
- 22 is divisible by 2: 22 = 2 x 11
- 11 is a prime number.
Therefore, the prime factorization of 88 is 2 x 2 x 2 x 11, or 2³ x 11.
Understanding the prime factorization is crucial because it allows us to easily determine all the factors of a number. Any factor of 88 will be a combination of the prime factors (2 and 11) raised to powers less than or equal to their powers in the prime factorization.
For instance:
- 2¹ = 2
- 2² = 4
- 2³ = 8
- 11¹ = 11
- 2¹ x 11¹ = 22
- 2² x 11¹ = 44
- 2³ x 11¹ = 88
This method efficiently generates all possible factors without missing any.
Beyond the Basics: Applications of Factors and Factorization
The concept of factors extends far beyond simply listing divisors of a number. It plays a crucial role in various areas of mathematics and its applications:
-
Greatest Common Divisor (GCD) and Least Common Multiple (LCM): Finding the GCD and LCM of two or more numbers is essential in simplifying fractions, solving algebraic equations, and working with rhythmic patterns in music. Prime factorization provides an efficient method for calculating GCD and LCM.
-
Cryptography: Prime factorization forms the basis of many modern cryptographic systems, including the widely used RSA algorithm. The difficulty of factoring large numbers into their prime components is what makes these systems secure.
-
Modular Arithmetic: Understanding factors is essential in modular arithmetic, a branch of number theory with applications in computer science, cryptography, and even music theory.
-
Algebraic Equations: Factoring polynomials is a crucial technique in solving algebraic equations and simplifying expressions. The same principles of factorization used for integers apply to polynomials.
-
Combinatorics and Probability: Factors are involved in calculating combinations and permutations, which are fundamental concepts in probability and statistics.
Exploring Number Patterns and Relationships: The Significance of 88
While finding the factors of 88 might seem like a simple exercise, exploring its properties can reveal interesting number patterns and relationships. For instance:
-
Abundant Number: 88 is an abundant number, meaning the sum of its proper divisors (all divisors except itself) is greater than the number itself. The sum of its proper divisors (1 + 2 + 4 + 8 + 11 + 22 + 44 = 92) is greater than 88.
-
Composite Number: 88 is a composite number because it has factors other than 1 and itself.
-
Relationship to other numbers: Exploring the relationship between 88 and other numbers, such as its multiples or numbers with similar prime factorizations, can reveal additional mathematical insights.
Conclusion: The Richness of Number Theory
The seemingly simple question of finding the factors of 88 serves as a gateway to a deeper understanding of number theory and its far-reaching applications. From the fundamental concepts of prime factorization to its role in advanced areas like cryptography, the significance of factors transcends the initial simplicity of the problem. This exploration highlights the beauty and intricacy inherent in the seemingly straightforward world of numbers. By understanding factors and their implications, we gain a richer appreciation for the underlying structure and elegance of mathematics itself. The journey from a simple question about the factors of 88 to the broader landscape of number theory demonstrates the captivating power of mathematical exploration.
Latest Posts
Latest Posts
-
Is 97 A Prime Or Composite
Apr 06, 2025
-
Evaluate The Indefinite Integral As An Infinite Series
Apr 06, 2025
-
What Is 20 Percent Of 25 Dollars
Apr 06, 2025
-
What Is The Least Common Multiple Of 8 And 20
Apr 06, 2025
-
How To Write 1300 On A Check
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about What Are The Factors For 88 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
