What Are The Factors Of 105
News Co
Apr 07, 2025 · 6 min read
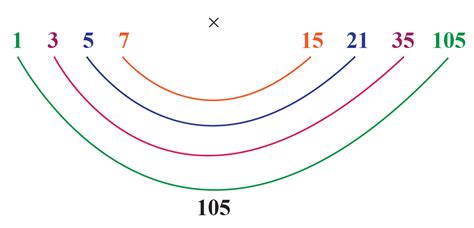
Table of Contents
- What Are The Factors Of 105
- Table of Contents
- What are the Factors of 105? A Deep Dive into Number Theory
- Understanding Factors and Divisibility
- The Prime Factorization Method: Unveiling the Building Blocks
- From Prime Factors to All Factors: A Systematic Approach
- Exploring Factor Properties: Even and Odd, Perfect Numbers, and More
- Applications of Factorization: Real-World Uses
- Beyond 105: Expanding the Understanding of Factors
- Advanced Concepts Related to Factors: A Glimpse into Number Theory
- Latest Posts
- Related Post
What are the Factors of 105? A Deep Dive into Number Theory
Finding the factors of a number might seem like a simple arithmetic task, but it opens a door to a fascinating world of number theory. Understanding factors is fundamental to many mathematical concepts, from simplifying fractions to solving complex equations. This article will delve into the factors of 105, exploring different methods to find them, their properties, and their significance within the broader context of mathematics.
Understanding Factors and Divisibility
Before we tackle the specific factors of 105, let's define some key terms. A factor (or divisor) of a number is a whole number that divides evenly into that number without leaving a remainder. For instance, 3 is a factor of 12 because 12 divided by 3 equals 4. The process of determining if one number is a factor of another is known as divisibility.
The Prime Factorization Method: Unveiling the Building Blocks
One of the most powerful ways to find all the factors of a number is through prime factorization. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (examples include 2, 3, 5, 7, 11, etc.). Prime factorization involves breaking down a number into its prime factors—the prime numbers that, when multiplied together, result in the original number.
Let's apply this method to 105:
- Start with the smallest prime number, 2: 105 is not divisible by 2 (it's an odd number).
- Try the next prime number, 3: 105 divided by 3 is 35. So, 3 is a factor.
- Now consider 35: 35 is not divisible by 3, but it is divisible by 5 (another prime number). 35 divided by 5 is 7.
- Finally, we have 7: 7 is a prime number.
Therefore, the prime factorization of 105 is 3 x 5 x 7.
From Prime Factors to All Factors: A Systematic Approach
Once we have the prime factorization, we can systematically find all the factors of 105. This involves considering all possible combinations of the prime factors.
- 1: The number 1 is always a factor of any number.
- 3: One of the prime factors.
- 5: Another prime factor.
- 7: The third prime factor.
- 3 x 5 = 15: The product of two prime factors.
- 3 x 7 = 21: The product of two prime factors.
- 5 x 7 = 35: The product of two prime factors.
- 3 x 5 x 7 = 105: The product of all prime factors (the number itself).
Therefore, the complete set of factors for 105 is 1, 3, 5, 7, 15, 21, 35, and 105.
Exploring Factor Properties: Even and Odd, Perfect Numbers, and More
The factors of 105 exhibit several interesting properties:
-
Odd Factors: All the factors of 105 are odd numbers. This is because 105 itself is an odd number, and the product of odd numbers is always odd.
-
Sum of Factors: The sum of the factors of 105 (1 + 3 + 5 + 7 + 15 + 21 + 35 + 105) equals 192. This sum is significant in certain number theory contexts, such as the study of perfect numbers (numbers whose sum of factors, excluding the number itself, is equal to the number). 105 is not a perfect number.
-
Number of Factors: 105 has eight factors. This is related to the exponents in its prime factorization. Since 105 = 3¹ x 5¹ x 7¹, the number of factors is calculated as (1+1)(1+1)(1+1) = 8. This formula works for any number whose prime factorization is known.
Applications of Factorization: Real-World Uses
Understanding factors and factorization isn't just an abstract mathematical exercise. It has numerous practical applications across various fields:
-
Simplifying Fractions: Finding the greatest common factor (GCF) of the numerator and denominator allows for simplifying fractions to their lowest terms. For example, if we have the fraction 21/105, finding that the GCF of 21 and 105 is 21 allows us to simplify the fraction to 1/5.
-
Solving Equations: Factorization is crucial in solving polynomial equations. For example, quadratic equations can often be solved by factoring the quadratic expression.
-
Cryptography: Factorization plays a vital role in modern cryptography, particularly in public-key cryptosystems like RSA. The security of these systems relies on the difficulty of factoring very large numbers into their prime factors.
-
Scheduling and Combinatorics: Factors are involved in solving problems related to scheduling, arranging items, and other combinatorics tasks where divisibility and grouping are important.
-
Geometry: Finding factors is relevant in geometric problems involving area and volume calculations. For example, determining if a rectangular area can be perfectly tiled with smaller squares often involves finding factors.
Beyond 105: Expanding the Understanding of Factors
While we've focused on 105, the principles and methods discussed here apply to finding the factors of any whole number. The prime factorization method remains a cornerstone approach, enabling us to understand the building blocks of a number and systematically derive all its factors. Mastering this skill not only enhances mathematical understanding but also equips you with tools applicable in diverse practical scenarios.
Advanced Concepts Related to Factors: A Glimpse into Number Theory
The exploration of factors can lead to more advanced areas within number theory:
-
Greatest Common Factor (GCF): The largest number that divides evenly into two or more numbers. Finding the GCF is essential for simplifying fractions and other mathematical operations. For example, the GCF of 105 and 70 is 35.
-
Least Common Multiple (LCM): The smallest number that is a multiple of two or more numbers. The LCM is crucial for solving problems involving fractions and finding common denominators. The LCM of 105 and 70 is 210.
-
Perfect Numbers: As mentioned earlier, these are numbers that equal the sum of their proper divisors (all divisors excluding the number itself). Exploring perfect numbers leads to deeper insights into the relationships between numbers and their factors.
-
Abundant and Deficient Numbers: These classifications categorize numbers based on the relationship between the number and the sum of its proper divisors. Abundant numbers have a sum of proper divisors greater than the number itself, while deficient numbers have a sum of proper divisors less than the number itself. 105 is an abundant number.
-
Highly Composite Numbers: These are numbers that have more divisors than any smaller positive integer. Understanding these numbers further deepens the study of divisibility and factorization.
By exploring the factors of 105, we've journeyed through fundamental concepts in number theory, discovering its practical implications and peeking into more advanced areas. The seemingly simple question of "What are the factors of 105?" unveils a rich mathematical landscape, showcasing the elegance and power of number theory. Further exploration of these concepts will undoubtedly lead to a greater appreciation of the intricate relationships between numbers.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Are The Factors Of 105 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.