What Are The Factors Of 125
News Co
Apr 05, 2025 · 6 min read
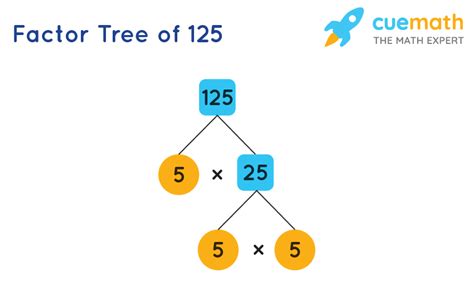
Table of Contents
What are the Factors of 125? A Deep Dive into Prime Factorization and Beyond
The seemingly simple question, "What are the factors of 125?" opens a door to a fascinating exploration of number theory, prime factorization, and the fundamental building blocks of mathematics. While the immediate answer might seem straightforward, delving deeper reveals a rich tapestry of mathematical concepts and their applications. This article will not only answer the question directly but also provide a comprehensive understanding of factors, prime numbers, and factorization techniques, all illustrated with examples relevant to 125 and beyond.
Understanding Factors
Before diving into the factors of 125 specifically, let's establish a clear understanding of what a factor is. In mathematics, a factor (or divisor) of a number is an integer that divides the number evenly, leaving no remainder. In simpler terms, it's a number that can be multiplied by another integer to produce the original number.
For example, the factors of 12 are 1, 2, 3, 4, 6, and 12, because:
- 1 x 12 = 12
- 2 x 6 = 12
- 3 x 4 = 12
Finding the Factors of 125
Now, let's focus on the number 125. To find its factors, we can systematically examine integers to see which ones divide 125 without leaving a remainder. We can start by checking the smallest positive integers:
- 1: 125 divided by 1 is 125, so 1 is a factor.
- 5: 125 divided by 5 is 25, so 5 is a factor.
- 25: 125 divided by 25 is 5, so 25 is a factor.
- 125: 125 divided by 125 is 1, so 125 is a factor.
Therefore, the factors of 125 are 1, 5, 25, and 125. Notice that the factors always come in pairs, except for perfect squares (like 25 in this case) which have one factor that pairs with itself.
Prime Factorization: The Building Blocks
The concept of prime numbers is crucial to understanding the fundamental structure of numbers. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. Examples include 2, 3, 5, 7, 11, and so on. Numbers that are not prime are called composite numbers.
Prime factorization is the process of expressing a composite number as a product of its prime factors. This is a unique representation for each composite number. Think of it as breaking down a number into its most fundamental building blocks.
Let's apply prime factorization to 125:
125 can be expressed as 5 x 25. However, 25 is not prime (it's 5 x 5). Therefore, the complete prime factorization of 125 is 5 x 5 x 5, or 5³.
This reveals that 125 is composed entirely of the prime number 5, repeated three times. This prime factorization is unique to 125; no other combination of prime numbers will result in 125.
The Significance of Prime Factorization
Prime factorization is more than just a mathematical exercise; it has significant applications in various fields:
-
Cryptography: Many encryption methods rely on the difficulty of factoring large numbers into their prime factors. This forms the basis of secure online transactions and data protection.
-
Number Theory: Prime factorization is fundamental to many areas of number theory, including the study of modular arithmetic, Diophantine equations, and the distribution of prime numbers.
-
Computer Science: Algorithms for prime factorization are used in various computational tasks, such as finding the greatest common divisor (GCD) of two numbers, which has applications in computer graphics and data compression.
-
Coding Theory: Prime numbers play a crucial role in error-correcting codes, which are used in data transmission and storage to ensure data integrity.
Beyond 125: Exploring Factorization Techniques
Understanding the factors of 125 provides a solid foundation for exploring factorization techniques for other numbers. Here are some useful methods:
-
Trial Division: This is the simplest method, where you systematically test each integer to see if it divides the number evenly. This works well for smaller numbers but becomes inefficient for larger ones.
-
Factor Tree: A visual method where you repeatedly break down the number into smaller factors until you reach only prime factors. This is a particularly helpful method for visualizing the prime factorization process.
-
Division by Prime Numbers: Start by dividing the number by the smallest prime number (2), then continue with the next prime number (3), and so on. Repeat until you have factored the number completely into prime numbers.
-
Using the Difference of Squares: This technique is useful when the number is a difference of two squares (e.g., a² - b² = (a+b)(a-b)).
-
Using the Sum or Difference of Cubes: Similar to the difference of squares, this can simplify factoring numbers that are sums or differences of cubes (e.g., a³ + b³ or a³ - b³).
These methods, when combined with a solid understanding of prime numbers and the unique nature of prime factorization, equip us with powerful tools for analyzing and manipulating numbers.
Practical Applications and Further Exploration
The ability to find factors and perform prime factorization is not confined to the realm of theoretical mathematics. It has numerous practical applications, including:
-
Simplifying Fractions: Finding the greatest common divisor (GCD) of the numerator and denominator allows for simplifying fractions to their lowest terms. This is done by finding the prime factorization of both the numerator and denominator, then identifying common prime factors.
-
Solving Algebraic Equations: Factoring polynomials is essential for solving many algebraic equations. The techniques used to factor numbers are directly applicable to factoring polynomials.
-
Understanding Number Patterns: Analyzing the factors of a number can reveal interesting patterns and relationships between numbers. This can lead to deeper insights into number theory and mathematical structures.
Further exploration can delve into:
-
The distribution of prime numbers: The prime number theorem provides an approximation of the number of primes less than a given number.
-
Mersenne primes: These are prime numbers of the form 2<sup>p</sup> - 1, where p is a prime number. The search for Mersenne primes is an active area of research.
-
Fermat primes: These are prime numbers of the form 2<sup>2<sup>n</sup></sup> + 1.
-
The Riemann Hypothesis: This unsolved problem in number theory is related to the distribution of prime numbers. Its solution would have profound implications for our understanding of prime numbers and many other areas of mathematics.
In conclusion, the seemingly simple question of finding the factors of 125 opens up a vast landscape of mathematical concepts and their applications. From understanding basic factors to mastering prime factorization and exploring advanced number theory concepts, the journey of numerical exploration is both enriching and endlessly fascinating. The principles discussed here extend far beyond the number 125, providing a solid foundation for tackling more complex mathematical problems and enhancing your understanding of the fundamental building blocks of numbers.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Are The Factors Of 125 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.