What Are The Factors Of 126
News Co
Apr 07, 2025 · 6 min read
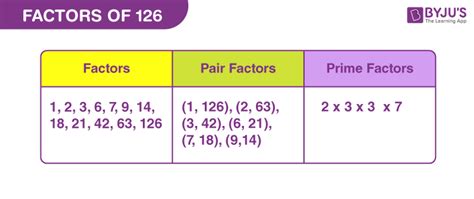
Table of Contents
What are the Factors of 126? A Deep Dive into Prime Factorization and Divisibility
Finding the factors of a number might seem like a simple mathematical task, but understanding the process reveals fundamental concepts in number theory. This article delves into the factors of 126, exploring various methods to identify them, examining the concept of prime factorization, and connecting this to broader mathematical ideas. We'll also discuss the practical applications of finding factors, demonstrating their relevance beyond basic arithmetic.
Understanding Factors and Divisibility
Before we jump into finding the factors of 126, let's establish a clear definition. A factor (or divisor) of a number is any integer that divides that number without leaving a remainder. In simpler terms, if you can divide a number by another number and get a whole number as the result, then the number you divided by is a factor. This relates directly to the concept of divisibility. A number is divisible by another number if the result of the division is a whole number.
For example, let's consider the number 12. The factors of 12 are 1, 2, 3, 4, 6, and 12. This is because 12 can be divided evenly by each of these numbers.
Finding the Factors of 126: A Step-by-Step Approach
There are several methods to find the factors of 126. Let's explore some of the most common and effective approaches:
Method 1: Systematic Division
This is a straightforward approach. We systematically divide 126 by each integer starting from 1, checking for whole number results.
- Divide by 1: 126 / 1 = 126 (1 and 126 are factors)
- Divide by 2: 126 / 2 = 63 (2 and 63 are factors)
- Divide by 3: 126 / 3 = 42 (3 and 42 are factors)
- Divide by 4: 126 / 4 = 31.5 (4 is not a factor)
- Divide by 5: 126 / 5 = 25.2 (5 is not a factor)
- Divide by 6: 126 / 6 = 21 (6 and 21 are factors)
- Divide by 7: 126 / 7 = 18 (7 and 18 are factors)
- Divide by 8: 126 / 8 = 15.75 (8 is not a factor)
- Divide by 9: 126 / 9 = 14 (9 and 14 are factors)
- Divide by 10: 126 / 10 = 12.6 (10 is not a factor)
- Divide by 11: 126 / 11 = 11.45 (11 is not a factor)
- Divide by 12: 126 / 12 = 10.5 (12 is not a factor)
- Divide by 13: 126 / 13 = 9.69 (13 is not a factor)
- Divide by 14: 126 / 14 = 9 (14 and 9 are factors – we've already found 9)
We can stop here because the next integer to test (15) is greater than the square root of 126 (approximately 11.22). Once we pass the square root, we'll simply find factor pairs we've already discovered in reverse order.
Therefore, the factors of 126 are: 1, 2, 3, 6, 7, 9, 14, 18, 21, 42, 63, and 126.
Method 2: Prime Factorization
Prime factorization is a more elegant and efficient method for finding all factors. It involves expressing the number as a product of its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself.
Let's find the prime factorization of 126:
- Divide by 2: 126 = 2 x 63
- Divide 63 by 3: 63 = 3 x 21
- Divide 21 by 3: 21 = 3 x 7
- 7 is a prime number.
Therefore, the prime factorization of 126 is 2 x 3 x 3 x 7, or 2 x 3² x 7.
From the prime factorization, we can systematically derive all factors. We can combine the prime factors in various ways to obtain all possible factors. For example:
- 2 x 3 = 6
- 2 x 7 = 14
- 2 x 3 x 3 = 18
- 2 x 3 x 7 = 42
- 3 x 3 = 9
- 3 x 7 = 21
- 3 x 3 x 7 = 63
- 2 x 3 x 3 x 7 = 126
- and the individual primes (2,3,7) and 1.
This method ensures we don't miss any factors.
The Significance of Prime Factorization
Prime factorization is not just a technique for finding factors; it's a fundamental concept in number theory with numerous applications:
-
Greatest Common Divisor (GCD): Finding the GCD of two or more numbers is crucial in simplifying fractions and solving various mathematical problems. Prime factorization makes finding the GCD significantly easier.
-
Least Common Multiple (LCM): The LCM is essential when working with fractions, particularly when adding or subtracting them. Prime factorization streamlines the process of finding the LCM.
-
Cryptography: Prime numbers and factorization play a critical role in modern cryptography, particularly in public-key cryptography systems like RSA. The difficulty of factoring large numbers into their prime components forms the basis of the security of these systems.
-
Modular Arithmetic: Modular arithmetic, used extensively in computer science and cryptography, relies heavily on the properties of prime numbers and factorization.
Applications of Factors in Real-World Scenarios
While finding the factors of 126 might seem purely academic, the concept of factors and divisibility has practical applications in various areas:
-
Dividing Resources: Imagine you have 126 items to distribute equally among groups. Knowing the factors of 126 helps determine the possible group sizes (1, 2, 3, 6, 7, 9, 14, 18, 21, 42, 63, 126).
-
Arranging Objects: Suppose you need to arrange 126 objects into a rectangular grid. The factors of 126 represent the possible dimensions of the grid (e.g., 2 rows by 63 columns, 7 rows by 18 columns, etc.).
-
Measurement and Conversion: Many measurement conversions involve using factors. For example, converting inches to feet or centimeters to meters requires understanding the factors relating the different units.
-
Scheduling and Time Management: Determining optimal scheduling often involves finding factors that allow for even distribution of tasks or resources over a given time period.
Beyond 126: Exploring Factorization of Larger Numbers
The methods discussed for finding the factors of 126 are applicable to numbers of any size, although larger numbers naturally require more computational effort. For extremely large numbers, sophisticated algorithms are employed, such as the general number field sieve, which is used in attempts to factor large numbers used in cryptography.
Conclusion: The Importance of Understanding Factors
Understanding the factors of a number, and particularly the method of prime factorization, is a cornerstone of mathematical understanding. While finding the factors of 126 might appear to be a simple exercise, the underlying concepts have far-reaching implications in various fields, from basic arithmetic and geometry to advanced areas like cryptography and computer science. The ability to efficiently find factors and understand prime factorization unlocks a deeper appreciation of the structure and properties of numbers. It's a skill that extends far beyond the classroom and plays a crucial role in numerous practical applications.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Are The Factors Of 126 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.