What Are The Prime Factors Of 102
News Co
Apr 16, 2025 · 5 min read
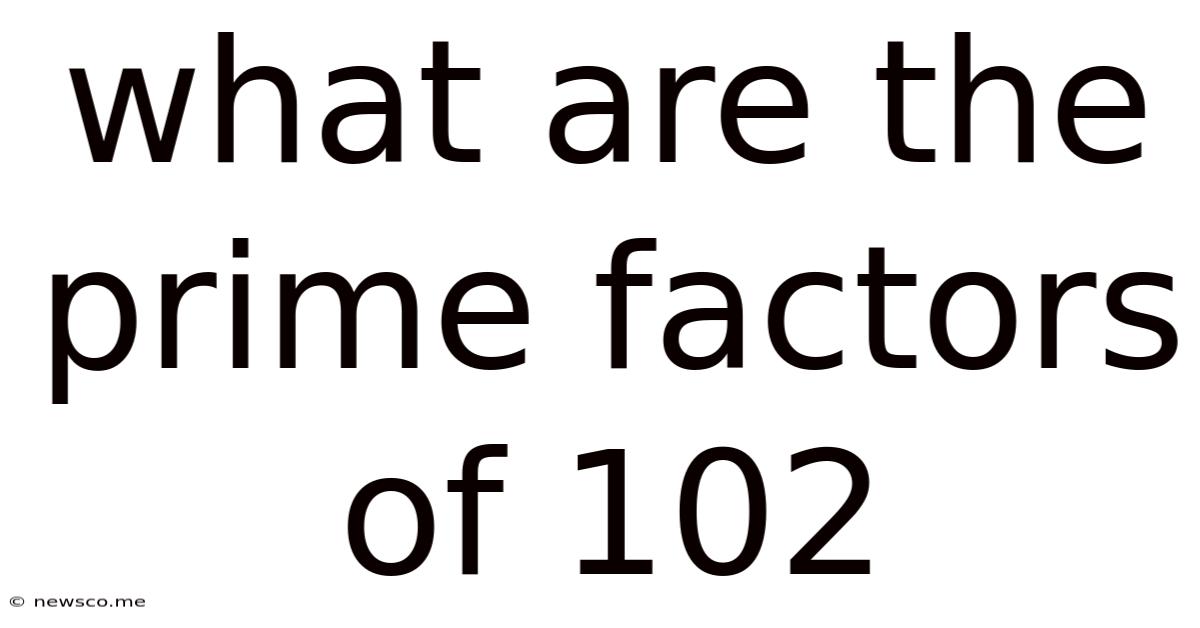
Table of Contents
What are the Prime Factors of 102? A Deep Dive into Prime Factorization
Finding the prime factors of a number might seem like a simple task, especially with a smaller number like 102. However, understanding the process thoroughly unlocks a deeper understanding of number theory and its applications in various fields, from cryptography to computer science. This article will not only determine the prime factors of 102 but also explore the underlying concepts and techniques involved in prime factorization, making it suitable for both beginners and those seeking a refresher on this fundamental mathematical concept.
Understanding Prime Numbers and Prime Factorization
Before diving into the prime factors of 102, let's establish a solid foundation.
What is a Prime Number?
A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. This means it's not divisible by any other whole number without leaving a remainder. The first few prime numbers are 2, 3, 5, 7, 11, 13, and so on. The sequence of prime numbers extends infinitely.
What is Prime Factorization?
Prime factorization is the process of breaking down a composite number (a number that is not prime) into its prime factors. Every composite number can be uniquely expressed as a product of prime numbers. This is known as the Fundamental Theorem of Arithmetic. For example, the prime factorization of 12 is 2 x 2 x 3 (or 2² x 3).
Finding the Prime Factors of 102: A Step-by-Step Approach
Now, let's determine the prime factors of 102. We'll use a systematic approach to ensure we find all the prime factors.
Step 1: Start with the Smallest Prime Number
The smallest prime number is 2. We check if 102 is divisible by 2. Since 102 is an even number, it's divisible by 2.
102 ÷ 2 = 51
Step 2: Continue with the Next Prime Number
Now we have 51. Is 51 divisible by 2? No, it's an odd number. Let's try the next prime number, 3. The sum of the digits of 51 (5 + 1 = 6) is divisible by 3, so 51 is divisible by 3.
51 ÷ 3 = 17
Step 3: Identify if the Result is Prime
We're left with 17. Is 17 a prime number? Yes, 17 is only divisible by 1 and itself.
Step 4: Write the Prime Factorization
Therefore, the prime factorization of 102 is 2 x 3 x 17.
Different Methods for Prime Factorization
While the method above is straightforward, other techniques can be employed, especially for larger numbers.
Factor Tree Method
The factor tree method is a visual approach to prime factorization. You start with the original number and branch out, repeatedly factoring until you're left with only prime numbers. For 102, a factor tree would look like this:
102
/ \
2 51
/ \
3 17
The prime factors at the end of the branches are 2, 3, and 17.
Repeated Division Method
The repeated division method involves repeatedly dividing the number by the smallest prime number that divides it evenly until you reach 1. This method is particularly efficient for larger numbers. For 102:
- 102 ÷ 2 = 51
- 51 ÷ 3 = 17
- 17 ÷ 17 = 1
The prime factors are the divisors used: 2, 3, and 17.
Applications of Prime Factorization
Prime factorization isn't just a mathematical curiosity; it has significant practical applications:
Cryptography
Prime numbers are fundamental to modern cryptography, particularly in RSA encryption, a widely used public-key cryptosystem. The security of RSA relies on the difficulty of factoring large numbers into their prime components. The larger the prime numbers used, the more secure the encryption.
Computer Science
Prime factorization plays a role in various algorithms and data structures in computer science. For instance, efficient algorithms for prime factorization are crucial for tasks like hash table design and data compression.
Number Theory
Prime factorization is a cornerstone of number theory, a branch of mathematics that deals with the properties of integers. Many important theorems and concepts in number theory are based on the unique prime factorization of integers.
Advanced Concepts Related to Prime Factorization
Let's delve into some more advanced concepts related to prime factorization:
Greatest Common Divisor (GCD) and Least Common Multiple (LCM)
Prime factorization is essential for efficiently calculating the greatest common divisor (GCD) and the least common multiple (LCM) of two or more numbers. The GCD is the largest number that divides all the given numbers without leaving a remainder, while the LCM is the smallest number that is a multiple of all the given numbers.
For example, to find the GCD and LCM of 102 and 136, we first find their prime factorizations:
- 102 = 2 x 3 x 17
- 136 = 2³ x 17
The GCD is found by taking the common prime factors with the lowest powers: 2¹ x 17 = 34.
The LCM is found by taking all the prime factors with the highest powers: 2³ x 3 x 17 = 408.
The Sieve of Eratosthenes
The Sieve of Eratosthenes is an ancient algorithm for finding all prime numbers up to a specified integer. It's a simple yet effective method for generating a list of prime numbers, which is helpful in various applications involving prime numbers.
Distribution of Prime Numbers
The distribution of prime numbers is a fascinating area of research in number theory. While there's no simple formula to predict the exact location of the next prime number, mathematicians have developed sophisticated techniques to estimate the number of primes within a given range. The Prime Number Theorem provides an approximation for the density of prime numbers.
Conclusion: The Prime Factors of 102 and Beyond
We've successfully determined that the prime factors of 102 are 2, 3, and 17. However, the journey of understanding prime factorization goes far beyond this single example. It's a fundamental concept with widespread implications across diverse fields. By grasping the techniques and applications discussed in this article, you'll enhance your mathematical understanding and gain valuable insights into the world of numbers and their properties. Remember, the seemingly simple act of finding the prime factors of a number opens doors to a rich and fascinating world of mathematical exploration.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Are The Prime Factors Of 102 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.