What Are The Prime Factors Of 104
News Co
Mar 18, 2025 · 4 min read
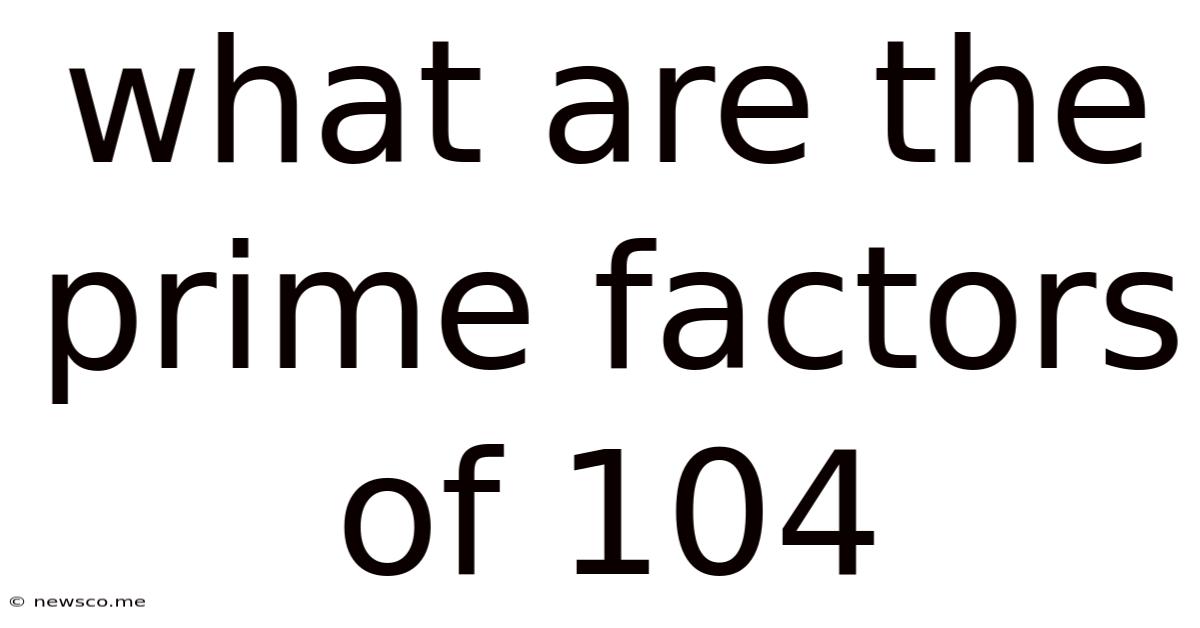
Table of Contents
What Are the Prime Factors of 104? A Deep Dive into Prime Factorization
Finding the prime factors of a number might seem like a simple mathematical exercise, but it's a fundamental concept with applications far beyond the classroom. Understanding prime factorization is crucial in various fields, from cryptography to number theory. This article delves into the process of finding the prime factors of 104, explaining the method, providing examples, and exploring the broader significance of prime factorization.
Understanding Prime Numbers and Prime Factorization
Before we tackle the prime factors of 104, let's establish a firm grasp of the core concepts.
Prime numbers are whole numbers greater than 1 that are only divisible by 1 and themselves. Examples include 2, 3, 5, 7, 11, and so on. A number that is not prime is called a composite number.
Prime factorization is the process of expressing a composite number as a product of its prime factors. Every composite number can be uniquely expressed as a product of prime numbers. This is known as the Fundamental Theorem of Arithmetic.
Finding the Prime Factors of 104: A Step-by-Step Guide
Now, let's find the prime factors of 104. We'll use a method called the factor tree.
-
Start with the smallest prime number: The smallest prime number is 2. We check if 104 is divisible by 2. Since 104 is an even number, it is divisible by 2.
-
Perform the division: 104 divided by 2 is 52.
-
Continue the process: Now we consider 52. 52 is also divisible by 2. 52 divided by 2 is 26.
-
Repeat until we reach a prime number: 26 is also divisible by 2, resulting in 13.
-
The final prime number: 13 is a prime number. We can't divide it further into smaller prime factors.
Therefore, the prime factorization of 104 is 2 x 2 x 2 x 13, which can also be written as 2³ x 13.
Visualizing the Prime Factorization with a Factor Tree
A factor tree provides a visual representation of the factorization process. For 104, the factor tree would look like this:
104
/ \
2 52
/ \
2 26
/ \
2 13
Each branch ends with a prime number. The prime factors are 2 (three times) and 13.
Applications of Prime Factorization
Prime factorization might seem like a purely theoretical concept, but it has several practical applications:
-
Cryptography: Many encryption methods rely heavily on prime numbers and their properties. The difficulty of factoring large numbers into their prime components is the basis of RSA encryption, one of the most widely used public-key cryptosystems.
-
Number Theory: Prime factorization is fundamental in number theory, a branch of mathematics concerned with the properties of numbers. Many theorems and conjectures in number theory are based on prime numbers and their distributions.
-
Computer Science: Prime factorization algorithms are used in various computer science applications, including efficient data structures and algorithms.
-
Coding Theory: Prime numbers play a role in error-correcting codes, which are used to detect and correct errors in data transmission.
-
Modular Arithmetic: Understanding prime factorization is crucial in modular arithmetic, which is widely used in cryptography and other areas.
Beyond 104: Exploring Other Prime Factorizations
Let's explore the prime factorization of a few more numbers to solidify our understanding:
Example 1: Prime Factorization of 72
- 72 is divisible by 2: 72 / 2 = 36
- 36 is divisible by 2: 36 / 2 = 18
- 18 is divisible by 2: 18 / 2 = 9
- 9 is divisible by 3: 9 / 3 = 3
- 3 is a prime number.
Therefore, the prime factorization of 72 is 2 x 2 x 2 x 3 x 3, or 2³ x 3².
Example 2: Prime Factorization of 150
- 150 is divisible by 2: 150 / 2 = 75
- 75 is divisible by 3: 75 / 3 = 25
- 25 is divisible by 5: 25 / 5 = 5
- 5 is a prime number.
Therefore, the prime factorization of 150 is 2 x 3 x 5 x 5, or 2 x 3 x 5².
Advanced Techniques for Prime Factorization
For larger numbers, the process of finding prime factors can become more complex. Advanced techniques and algorithms exist to handle such cases efficiently, including:
-
Trial Division: This is a basic method, but it becomes computationally expensive for very large numbers.
-
Sieve of Eratosthenes: This is an algorithm for finding all prime numbers up to a specified integer.
-
Pollard's Rho Algorithm: A probabilistic algorithm used for factoring composite numbers.
-
General Number Field Sieve (GNFS): The most efficient known algorithm for factoring very large numbers.
Conclusion: The Enduring Importance of Prime Factors
The seemingly simple act of finding the prime factors of a number, like 104, opens a gateway to a fascinating world of mathematics with far-reaching consequences. From securing online transactions to advancing our understanding of numbers themselves, prime factorization remains a vital concept across various fields. Understanding the process, its applications, and the advanced techniques involved provides a valuable foundation for anyone interested in mathematics, computer science, or cryptography. The seemingly simple question, "What are the prime factors of 104?" thus reveals a depth and significance that extends far beyond its initial appearance.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Are The Prime Factors Of 104 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.