What Are The Prime Factors Of 124
News Co
Apr 25, 2025 · 5 min read
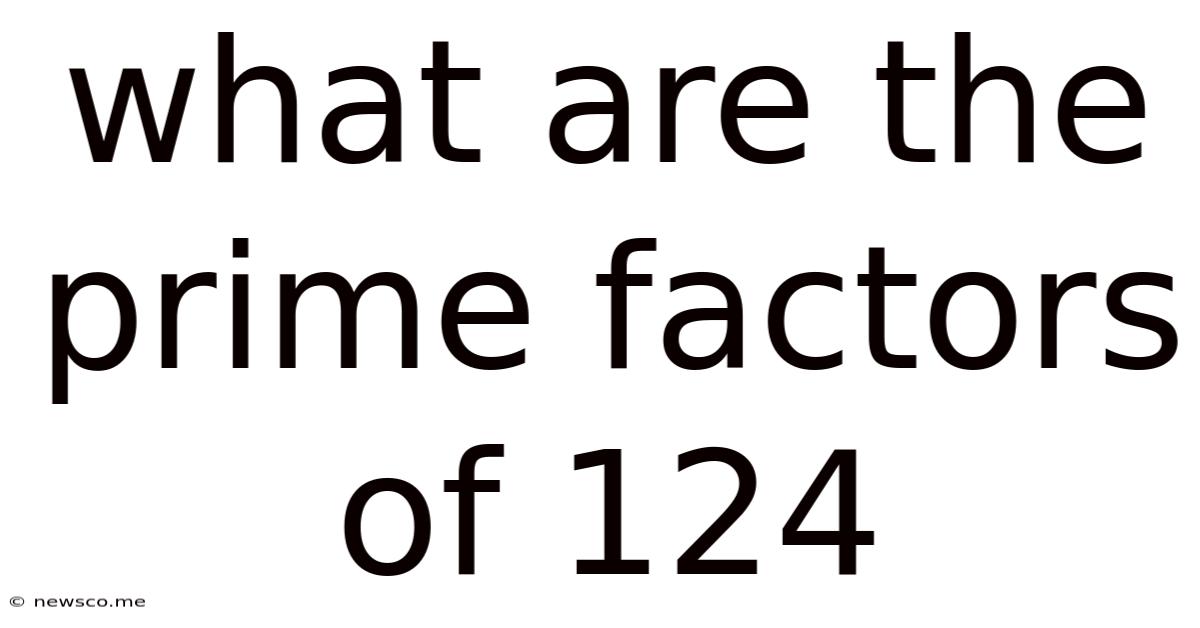
Table of Contents
What Are the Prime Factors of 124? A Deep Dive into Prime Factorization
Finding the prime factors of a number might seem like a simple mathematical exercise, but understanding the process unlocks a deeper appreciation of number theory and its applications in various fields like cryptography and computer science. This article delves into the fascinating world of prime factorization, using the number 124 as our example. We'll not only determine its prime factors but also explore the underlying concepts and techniques involved.
Understanding Prime Numbers and Prime Factorization
Before we tackle 124, let's establish a solid foundation. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. The first few prime numbers are 2, 3, 5, 7, 11, and so on. Prime numbers are the building blocks of all other numbers.
Prime factorization, also known as prime decomposition, is the process of finding the prime numbers that multiply together to make a given number. Every composite number (a number that's not prime) can be expressed as a unique product of prime numbers. This unique representation is fundamental to many mathematical concepts.
Finding the Prime Factors of 124: A Step-by-Step Approach
Now, let's apply this knowledge to find the prime factors of 124. We can use a method called the factor tree to visually represent the process.
-
Start with the original number: We begin with 124.
-
Find the smallest prime factor: The smallest prime number is 2. Since 124 is an even number, it's divisible by 2. We divide 124 by 2: 124 ÷ 2 = 62.
-
Continue the process: Now we work with the result, 62. Again, 62 is an even number, divisible by 2: 62 ÷ 2 = 31.
-
Identify the prime factor: 31 is a prime number. It's only divisible by 1 and itself.
-
Express the prime factorization: We've reached a prime number, so we can stop. The prime factorization of 124 is 2 x 2 x 31, or 2² x 31.
Therefore, the prime factors of 124 are 2 and 31.
Visualizing the Process with a Factor Tree
A factor tree provides a clear visual representation of the factorization process. For 124, the factor tree would look like this:
124
/ \
2 62
/ \
2 31
Each branch represents a division by a prime factor, until we reach only prime numbers at the leaves of the tree.
Beyond the Factor Tree: Other Methods for Prime Factorization
While the factor tree is a simple and intuitive method, especially for smaller numbers, other techniques become more efficient for larger numbers. These include:
-
Division by Primes: Systematically divide the number by successive prime numbers (2, 3, 5, 7, etc.) until you reach 1. The prime numbers that divide evenly are the prime factors.
-
Trial Division: This is a similar method to division by primes, but instead of strictly following the prime number sequence, you test for divisibility by small numbers.
-
Sieve of Eratosthenes: This is a powerful algorithm for finding all prime numbers up to a specified limit. While it doesn't directly factor a specific number, it's helpful for generating a list of primes to test for divisibility.
-
Advanced Algorithms: For extremely large numbers, sophisticated algorithms like the general number field sieve are used. These are computationally intensive but necessary for factoring very large composite numbers, which is crucial in cryptography.
Applications of Prime Factorization
The seemingly simple process of prime factorization has profound applications in various fields:
-
Cryptography: Many modern encryption systems rely on the difficulty of factoring very large numbers into their prime factors. The security of RSA encryption, for instance, depends on the computational infeasibility of factoring the product of two large prime numbers.
-
Computer Science: Prime factorization is used in hash table algorithms, which are essential data structures in computer programming.
-
Number Theory: Prime factorization is a cornerstone of number theory, a branch of mathematics that studies the properties of integers. Many advanced theorems and conjectures in number theory depend on the understanding of prime factorization.
-
Coding Theory: Error-correcting codes, which ensure reliable data transmission, often utilize properties of prime numbers and prime factorization.
Exploring the Uniqueness of Prime Factorization: The Fundamental Theorem of Arithmetic
A crucial aspect of prime factorization is its uniqueness. The Fundamental Theorem of Arithmetic states that every integer greater than 1 can be represented uniquely as a product of prime numbers (disregarding the order of the factors). This means that no matter what method you use to factor a number, you'll always arrive at the same set of prime factors. This uniqueness is fundamental to many mathematical proofs and applications.
Practical Applications and Further Exploration
Understanding prime factorization extends beyond theoretical mathematics. Consider these practical applications:
-
Simplifying Fractions: When reducing fractions to their simplest form, prime factorization helps identify common factors in the numerator and denominator.
-
Finding the Least Common Multiple (LCM) and Greatest Common Divisor (GCD): Prime factorization simplifies the calculation of the LCM and GCD of two or more numbers.
-
Solving Diophantine Equations: Certain types of Diophantine equations (equations where only integer solutions are sought) can be solved using techniques based on prime factorization.
Conclusion: The Enduring Importance of Prime Factors
The seemingly simple question, "What are the prime factors of 124?" opens a door to a rich and complex world of number theory and its practical applications. Understanding prime factorization is not merely an academic exercise; it's a fundamental concept with far-reaching consequences in cryptography, computer science, and other fields. By mastering the techniques and appreciating the underlying principles, you gain valuable insights into the structure of numbers and their profound impact on our technological world. The seemingly simple task of finding the prime factors of 124 (2² x 31) serves as a gateway to exploring the fascinating world of prime numbers and their significant role in mathematics and beyond. The journey of understanding prime factorization is a continuous one, offering endless opportunities for exploration and discovery.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Are The Prime Factors Of 124 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.