What Are The Prime Factors Of 135
News Co
Apr 23, 2025 · 5 min read
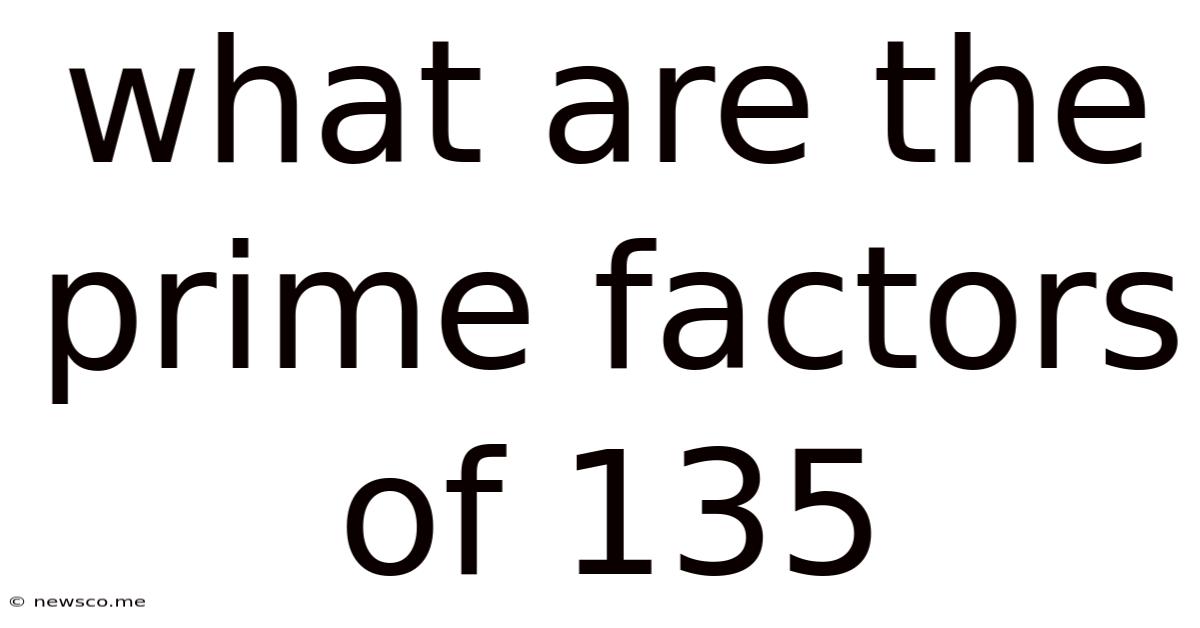
Table of Contents
What Are the Prime Factors of 135? A Deep Dive into Prime Factorization
Finding the prime factors of a number might seem like a simple mathematical exercise, but understanding the process unlocks a deeper appreciation for number theory and its applications in various fields like cryptography and computer science. This article will explore the prime factorization of 135 in detail, explaining the method, demonstrating different approaches, and highlighting the importance of prime numbers in mathematics.
Understanding Prime Numbers and Prime Factorization
Before diving into the prime factors of 135, let's establish a solid foundation. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. The first few prime numbers are 2, 3, 5, 7, 11, 13, and so on. A number that is not prime is called a composite number.
Prime factorization is the process of expressing a composite number as a product of its prime factors. This representation is unique for every composite number (excluding the order of the factors). This uniqueness is fundamental to many mathematical concepts. For example, it forms the basis for the greatest common divisor (GCD) and least common multiple (LCM) calculations, crucial in simplifying fractions and solving various algebraic problems.
Finding the Prime Factors of 135: The Method
There are several methods to find the prime factors of 135. Let's explore two common approaches:
Method 1: The Factor Tree Method
The factor tree method is a visual approach that's particularly useful for beginners. We start by finding any two factors of 135 and branching out. We continue this process until all branches end in prime numbers.
-
Start with 135: We can begin by noticing that 135 is divisible by 5 (since it ends in 5). So, we can write 135 as 5 x 27.
-
Factor 27: Now, we need to find the factors of 27. 27 is divisible by 3 (since the sum of its digits, 2 + 7 = 9, is divisible by 3). So, 27 can be written as 3 x 9.
-
Factor 9: 9 is also divisible by 3, giving us 3 x 3.
-
Prime Factors: We've reached prime numbers at the end of all branches: 5, 3, and 3.
Therefore, the prime factorization of 135 is 3 x 3 x 3 x 5, or 3³ x 5. We can represent this visually as a factor tree:
135
/ \
5 27
/ \
3 9
/ \
3 3
Method 2: Repeated Division by Prime Numbers
This method involves systematically dividing the number by the smallest prime number possible until we reach 1.
-
Divide by 3: 135 divided by 3 is 45.
-
Divide by 3 again: 45 divided by 3 is 15.
-
Divide by 3 again: 15 divided by 3 is 5.
-
Divide by 5: 5 divided by 5 is 1.
We've repeatedly divided by prime numbers (3 and 5) until we reached 1. The prime factors are the numbers we used to divide: 3, 3, 3, and 5.
This gives us the same prime factorization as before: 3³ x 5.
The Significance of Prime Factorization
The prime factorization of 135, and indeed of any number, isn't just a mathematical curiosity. It has several significant applications:
1. Greatest Common Divisor (GCD) and Least Common Multiple (LCM) Calculations
Finding the GCD and LCM of two or more numbers is simplified significantly using prime factorization. To find the GCD, we identify the common prime factors with the lowest exponents. To find the LCM, we use all prime factors with the highest exponents.
For instance, let's find the GCD and LCM of 135 and 90.
-
Prime factorization of 135: 3³ x 5
-
Prime factorization of 90: 2 x 3² x 5
-
GCD(135, 90): The common prime factors are 3 and 5. The lowest exponent of 3 is 2, and the lowest exponent of 5 is 1. Therefore, GCD(135, 90) = 3² x 5 = 45.
-
LCM(135, 90): We take all prime factors with the highest exponents: 2¹ x 3³ x 5¹ = 270.
2. Cryptography
Prime numbers are the cornerstone of many modern cryptographic systems. Algorithms like RSA encryption rely on the difficulty of factoring very large composite numbers into their prime factors. The security of these systems depends on the computational infeasibility of factoring extremely large numbers, making data transmission secure.
3. Modular Arithmetic and Number Theory
Prime factorization plays a crucial role in various branches of number theory, such as modular arithmetic. Understanding prime factorization allows for the solving of complex number theory problems and equations.
4. Simplifying Fractions
Prime factorization is essential for simplifying fractions to their lowest terms. By finding the prime factors of both the numerator and the denominator, we can cancel out common factors, reducing the fraction to its simplest form.
For example, the fraction 135/90 can be simplified using the GCD we calculated earlier: 135/90 = (3² x 5) / (2 x 3² x 5) = 3/2.
Beyond 135: Exploring Further
While we've focused on 135, the principles of prime factorization apply to all composite numbers. Understanding the process allows you to tackle the prime factorization of larger and more complex numbers. The more you practice, the faster and more efficient you become at identifying prime factors.
Conclusion: The Importance of Prime Numbers and Factorization
The seemingly simple task of finding the prime factors of 135 reveals a deeper understanding of fundamental mathematical concepts. From simplifying fractions to securing online transactions, the significance of prime numbers and prime factorization extends far beyond the classroom. Mastering this technique opens doors to a richer appreciation of number theory and its powerful applications in various fields. So, the next time you encounter a number, consider its prime factorization—it may hold a hidden key to a fascinating mathematical world.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Are The Prime Factors Of 135 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.