What Are The Prime Factors Of 140
News Co
Apr 23, 2025 · 4 min read
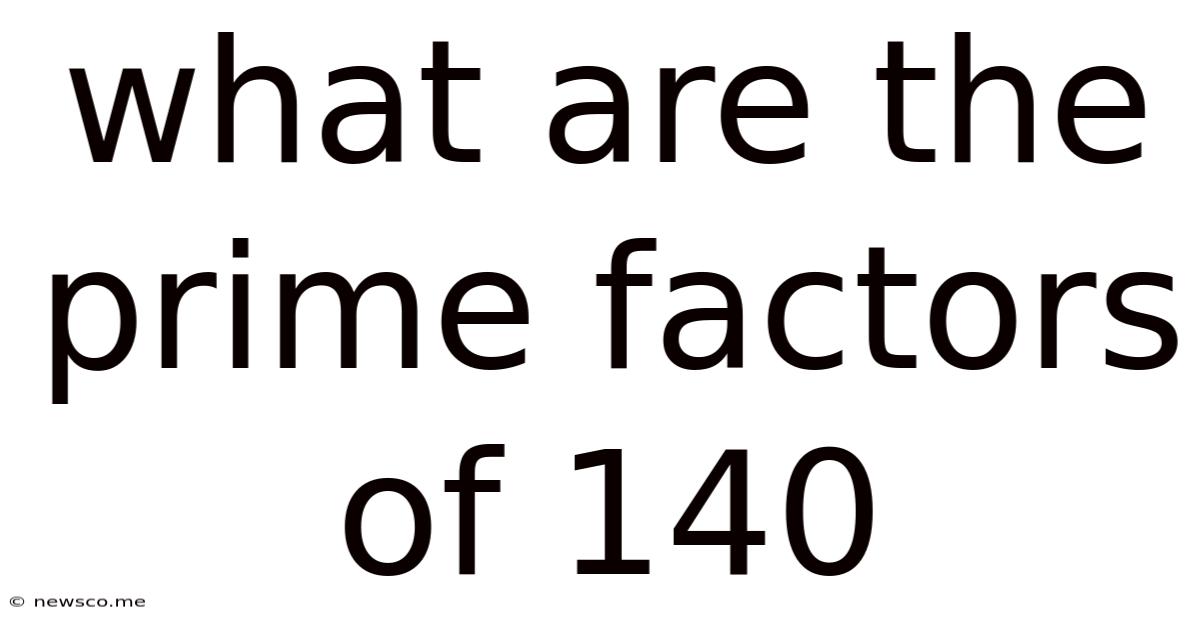
Table of Contents
What Are the Prime Factors of 140? A Deep Dive into Prime Factorization
Finding the prime factors of a number might seem like a simple mathematical exercise, but understanding the process reveals fundamental concepts in number theory and has practical applications in various fields, from cryptography to computer science. This article delves into the prime factorization of 140, explaining the method step-by-step and exploring the broader implications of prime numbers and their factorization.
Understanding Prime Numbers
Before we tackle the prime factorization of 140, let's solidify our understanding of prime numbers. A prime number is a natural number greater than 1 that is not a product of two smaller natural numbers. In simpler terms, a prime number is only divisible by 1 and itself. The first few prime numbers are 2, 3, 5, 7, 11, 13, and so on. The number 1 is not considered a prime number.
The fundamental theorem of arithmetic states that every integer greater than 1 can be represented uniquely as a product of prime numbers, disregarding the order of the factors. This unique representation is crucial in various mathematical applications.
Methods for Finding Prime Factors
Several methods exist for finding the prime factors of a number. Let's explore two common approaches:
1. The Factor Tree Method
This visual method is excellent for beginners and provides a clear understanding of the factorization process. We start by finding any two factors of the number and branch them off. We continue this process for each factor until all the branches end in prime numbers.
Let's apply this to 140:
- 140 can be factored into 2 x 70.
- 70 can be factored into 2 x 35.
- 35 can be factored into 5 x 7.
Both 5 and 7 are prime numbers. Therefore, the prime factorization of 140 using the factor tree method is 2 x 2 x 5 x 7, which can be written more concisely as 2² x 5 x 7.
2. Repeated Division by Prime Numbers
This method is more systematic and efficient for larger numbers. We start by dividing the number by the smallest prime number (2), and continue dividing by 2 until it's no longer divisible. Then, we move to the next prime number (3), and so on.
Let's apply this to 140:
- 140 ÷ 2 = 70
- 70 ÷ 2 = 35
- 35 is not divisible by 2, so we move to the next prime number, 3. 35 is not divisible by 3.
- 35 ÷ 5 = 7
- 7 is a prime number.
Therefore, the prime factorization of 140 using repeated division is 2 x 2 x 5 x 7, or 2² x 5 x 7.
The Prime Factorization of 140: 2² x 5 x 7
Both methods lead to the same result: the prime factorization of 140 is 2² x 5 x 7. This means that 140 can be expressed uniquely as the product of two 2s, one 5, and one 7. This unique representation is fundamental in many mathematical operations.
Applications of Prime Factorization
The seemingly simple process of finding prime factors has surprisingly far-reaching applications:
1. Greatest Common Divisor (GCD) and Least Common Multiple (LCM)
Prime factorization is crucial for finding the greatest common divisor (GCD) and the least common multiple (LCM) of two or more numbers. The GCD is the largest number that divides all the given numbers without leaving a remainder, while the LCM is the smallest number that is a multiple of all the given numbers.
For instance, finding the GCD and LCM of 140 and another number becomes significantly easier once we know its prime factorization.
2. Cryptography
Prime numbers and their factorization play a vital role in modern cryptography, particularly in public-key cryptography systems like RSA. The security of these systems relies on the difficulty of factoring very large numbers into their prime factors. The larger the numbers, the more computationally intensive the factorization becomes, making it practically impossible to break the encryption within a reasonable timeframe.
3. Computer Science
Prime factorization is used in various algorithms in computer science, including algorithms for efficient data compression, hashing, and random number generation. Understanding prime numbers is essential for developing robust and efficient computer systems.
4. Number Theory
Prime factorization is a cornerstone of number theory, a branch of mathematics that studies the properties of integers. It forms the basis for numerous theorems and concepts within this field. For example, the distribution of prime numbers is an ongoing area of research with significant implications for various mathematical areas.
Conclusion
Finding the prime factors of 140, while seemingly a straightforward task, illustrates the fundamental importance of prime numbers in mathematics and its applications. The unique prime factorization of every integer is a cornerstone concept that underpins many important algorithms and cryptographic systems. Mastering prime factorization enhances mathematical understanding and opens doors to exploring more advanced mathematical concepts. The ability to swiftly and accurately determine prime factors is a valuable skill with applications far beyond the classroom. The method, whether using a factor tree or repeated division, provides a clear path to understanding the building blocks of numbers and their unique compositions.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Are The Prime Factors Of 140 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.