What Are The Prime Factors Of 160
News Co
Apr 16, 2025 · 5 min read
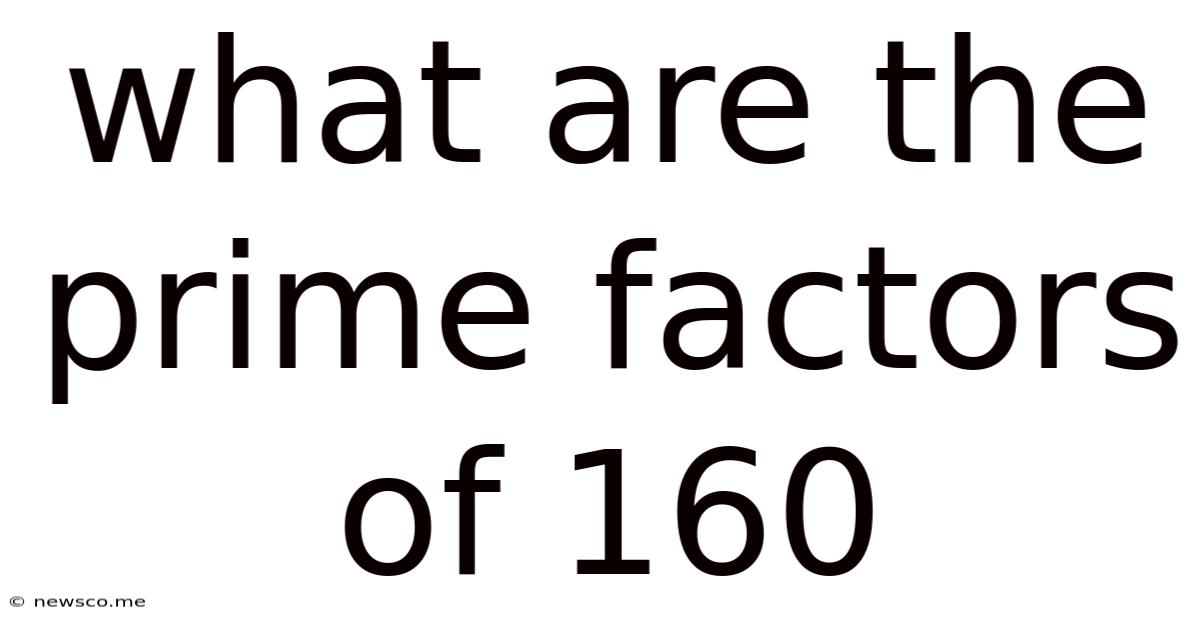
Table of Contents
What Are the Prime Factors of 160? A Deep Dive into Prime Factorization
Finding the prime factors of a number might seem like a simple mathematical exercise, but understanding the process reveals fundamental concepts in number theory and has practical applications in various fields, from cryptography to computer science. This article will not only determine the prime factors of 160 but will also explore the broader concept of prime factorization, its methods, and its significance.
Understanding Prime Numbers and Prime Factorization
Before diving into the prime factors of 160, let's establish a solid foundation. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. The first few prime numbers are 2, 3, 5, 7, 11, 13, and so on. Numbers that are not prime are called composite numbers.
Prime factorization is the process of expressing a composite number as a product of its prime factors. This representation is unique for every composite number; that is, every composite number can be expressed as a product of prime numbers in only one way (disregarding the order of the factors). This uniqueness is crucial and is known as the Fundamental Theorem of Arithmetic.
Finding the Prime Factors of 160: A Step-by-Step Approach
There are several methods to find the prime factors of a number. Let's explore a common and intuitive approach using the factor tree method:
-
Start with the smallest prime number: We begin by dividing 160 by the smallest prime number, which is 2. 160 divided by 2 is 80.
-
Continue dividing by prime numbers: Now we work with 80. Again, it's divisible by 2, resulting in 40.
-
Repeat the process: We continue dividing by 2: 40 divided by 2 is 20, and 20 divided by 2 is 10, and 10 divided by 2 is 5.
-
Reaching a prime number: We've reached 5, which is a prime number. This signifies the end of our factorization.
We can represent this process visually using a factor tree:
160
/ \
2 80
/ \
2 40
/ \
2 20
/ \
2 10
/ \
2 5
Therefore, the prime factorization of 160 is 2 x 2 x 2 x 2 x 2 x 5, or 2<sup>5</sup> x 5.
Alternative Methods for Prime Factorization
While the factor tree method is visually intuitive, especially for smaller numbers, other methods are more efficient for larger numbers. Let's explore a couple of them:
1. Repeated Division: This method involves repeatedly dividing the number by the smallest prime number until it's no longer divisible. Then, you move to the next smallest prime number and repeat the process. This method is particularly suitable for numbers that have a lot of small prime factors.
2. Division by Primes: You systematically try dividing the number by each prime number, starting with 2, then 3, 5, 7, and so on. Each time you successfully divide, you record the prime factor and continue with the quotient. You repeat until the quotient becomes 1.
The Significance of Prime Factorization
Beyond its use in basic arithmetic, prime factorization holds significant importance in several areas:
1. Cryptography: The difficulty of factoring large numbers into their prime factors is the foundation of many modern cryptographic systems, like RSA encryption. The security of these systems relies on the computational infeasibility of factoring very large composite numbers.
2. Computer Science: Prime numbers and prime factorization are used in various algorithms and data structures in computer science. For example, they play a critical role in hash functions and certain types of sorting algorithms.
3. Number Theory: Prime factorization is a central concept in number theory, a branch of mathematics that deals with the properties of integers. It forms the basis for many theorems and conjectures in number theory.
4. Abstract Algebra: Prime factorization extends its influence to abstract algebra, where it helps in understanding the structure of rings and ideals.
Error Handling and Dealing with Large Numbers
When dealing with larger numbers, manual methods become tedious. For such cases, software and programming languages offer efficient algorithms for prime factorization. These algorithms are optimized to handle large numbers and provide accurate results in a reasonable time. It's also important to have error handling in place, especially when dealing with user input to prevent unexpected program crashes or incorrect results. For instance, a program should handle cases where the input is not a positive integer or where the number is too large to factor within a reasonable timeframe.
Practical Applications and Examples
Let's consider some practical applications and examples related to prime factorization:
1. Simplifying Fractions: Prime factorization is crucial for simplifying fractions to their lowest terms. By finding the prime factors of the numerator and denominator, you can identify common factors and cancel them out.
2. Finding the Least Common Multiple (LCM) and Greatest Common Divisor (GCD): Prime factorization simplifies the calculation of LCM and GCD, which are important in various mathematical and practical problems involving fractions, ratios, and scheduling.
3. Solving Diophantine Equations: Prime factorization is often essential in solving Diophantine equations, which are polynomial equations with integer solutions.
Conclusion: The Enduring Importance of Prime Factorization
The prime factorization of 160, while seemingly a simple problem, serves as a gateway to understanding a fundamental concept in number theory with far-reaching implications. From the seemingly abstract realm of mathematics to the practical applications in cryptography and computer science, the ability to efficiently factor numbers into their prime components remains a crucial skill and an active area of research. The methods discussed, from the straightforward factor tree to more advanced algorithmic approaches, highlight the diverse ways we can unravel the structure of numbers and utilize this knowledge to solve complex problems. The journey into prime factorization is not just about finding the prime factors of 160; it’s about appreciating the elegance and power of mathematical concepts and their profound influence on our world.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Are The Prime Factors Of 160 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.