What Are The Prime Factors Of 360
News Co
Apr 06, 2025 · 5 min read
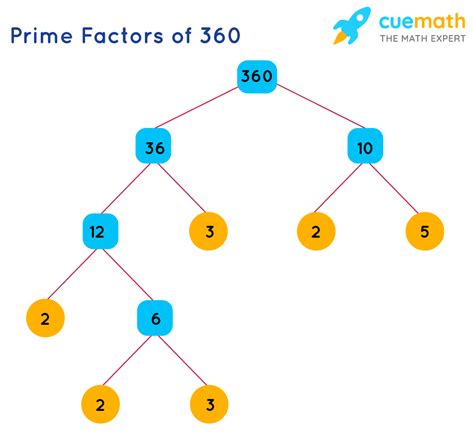
Table of Contents
- What Are The Prime Factors Of 360
- Table of Contents
- What Are the Prime Factors of 360? A Deep Dive into Prime Factorization
- Understanding Prime Numbers and Prime Factorization
- Finding the Prime Factors of 360: Step-by-Step
- Significance of Prime Factorization
- Properties of the Number 360
- Beyond the Basics: Exploring Advanced Concepts
- Conclusion: The Power of Prime Factorization
- Latest Posts
- Related Post
What Are the Prime Factors of 360? A Deep Dive into Prime Factorization
Finding the prime factors of a number is a fundamental concept in number theory, crucial for understanding various mathematical concepts and applications. This article will thoroughly explore the prime factorization of 360, explaining the process step-by-step, and delving into the significance of prime numbers and prime factorization in mathematics and beyond. We'll also look at different methods to find prime factors, and touch upon some interesting properties related to the number 360.
Understanding Prime Numbers and Prime Factorization
Before we dive into the prime factorization of 360, let's refresh our understanding of prime numbers and the concept of prime factorization.
What is a Prime Number?
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. In simpler terms, it's only divisible by 1 and itself. The first few prime numbers are 2, 3, 5, 7, 11, 13, and so on. The number 2 is the only even prime number; all other even numbers are divisible by 2.
What is Prime Factorization?
Prime factorization, also known as prime decomposition, is the process of finding the prime numbers that, when multiplied together, will result in the original number. Every composite number (a number greater than 1 that is not prime) can be uniquely expressed as a product of prime numbers. This is known as the Fundamental Theorem of Arithmetic.
Finding the Prime Factors of 360: Step-by-Step
Now, let's embark on finding the prime factors of 360 using a systematic approach:
Method 1: Repeated Division
This is a straightforward method. We repeatedly divide the number by the smallest prime number possible until we are left with 1.
- Start with the smallest prime number, 2: 360 ÷ 2 = 180
- Continue dividing by 2: 180 ÷ 2 = 90
- Continue dividing by 2: 90 ÷ 2 = 45
- Now, 2 doesn't divide 45. Move to the next prime number, 3: 45 ÷ 3 = 15
- Continue dividing by 3: 15 ÷ 3 = 5
- The next prime number is 5, which divides 5: 5 ÷ 5 = 1
We've reached 1, meaning we've found all the prime factors. Therefore, the prime factorization of 360 is 2 x 2 x 2 x 3 x 3 x 5, which can be written more concisely as 2³ x 3² x 5.
Method 2: Factor Tree
The factor tree method provides a visual representation of the factorization process.
- Start by expressing 360 as a product of any two factors. For example, 360 = 36 x 10.
- Break down 36 and 10 into their factors. 36 = 6 x 6, and 10 = 2 x 5.
- Further break down 6 into 2 x 3.
- Continue this process until all the factors are prime numbers.
Here's a visual representation of the factor tree for 360:
360
/ \
36 10
/ \ / \
6 6 2 5
/ \ / \
2 3 2 3
The prime factors are 2, 2, 2, 3, 3, and 5, leading to the same prime factorization as before: 2³ x 3² x 5.
Significance of Prime Factorization
Prime factorization is more than just a mathematical exercise; it has significant applications in various areas:
-
Cryptography: The security of many encryption algorithms relies heavily on the difficulty of factoring large numbers into their prime factors. RSA encryption, widely used in online security, is a prime example.
-
Number Theory: Prime factorization is fundamental to many concepts in number theory, such as modular arithmetic, congruences, and the study of Diophantine equations.
-
Computer Science: Algorithms for prime factorization are crucial in computer science, particularly in areas like cryptography and data compression.
-
Mathematics Education: Understanding prime factorization is essential for mastering other mathematical concepts, such as fractions, greatest common divisor (GCD), and least common multiple (LCM).
Properties of the Number 360
The number 360 holds some interesting properties, some of which are linked to its prime factorization:
-
Highly Composite Number: 360 is a highly composite number, meaning it has more divisors than any smaller positive integer. Its prime factorization (2³ x 3² x 5) contributes to this high number of divisors.
-
Divisibility: Because of its prime factorization, 360 is divisible by many numbers. It's divisible by 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180, and 360.
-
Historical Significance: The number 360 has historical significance, often used in ancient civilizations as an approximation of the number of days in a year. This likely contributed to its prominence in Babylonian mathematics and astronomy.
-
Geometry: 360 degrees make up a full circle. This is a widely used convention in geometry and trigonometry.
Beyond the Basics: Exploring Advanced Concepts
While the prime factorization of 360 might seem simple, it serves as a gateway to more advanced concepts:
-
Greatest Common Divisor (GCD): Knowing the prime factorization allows for efficient calculation of the GCD of 360 and other numbers. The GCD is the largest number that divides both numbers without leaving a remainder.
-
Least Common Multiple (LCM): Similarly, the prime factorization helps determine the LCM, the smallest number that is a multiple of both numbers.
-
Modular Arithmetic: Understanding prime factorization is crucial for working with modular arithmetic, where operations are performed within a specific modulus (remainder).
Conclusion: The Power of Prime Factorization
The prime factorization of 360, 2³ x 3² x 5, is not just a result of a simple calculation. It unlocks a deeper understanding of number theory, provides insights into the structure of numbers, and has significant implications in various fields. From cryptography to geometry, the concept of prime factorization plays a vital role. Understanding this foundational concept opens doors to more complex and fascinating areas of mathematics and its applications. By mastering this fundamental skill, you gain a stronger foundation in mathematics and its powerful applications across diverse disciplines. Continue exploring the wonders of prime numbers and their factorization; you'll be amazed at the discoveries you can make.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Are The Prime Factors Of 360 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.