What Are The Prime Factors Of 700
News Co
Apr 03, 2025 · 4 min read
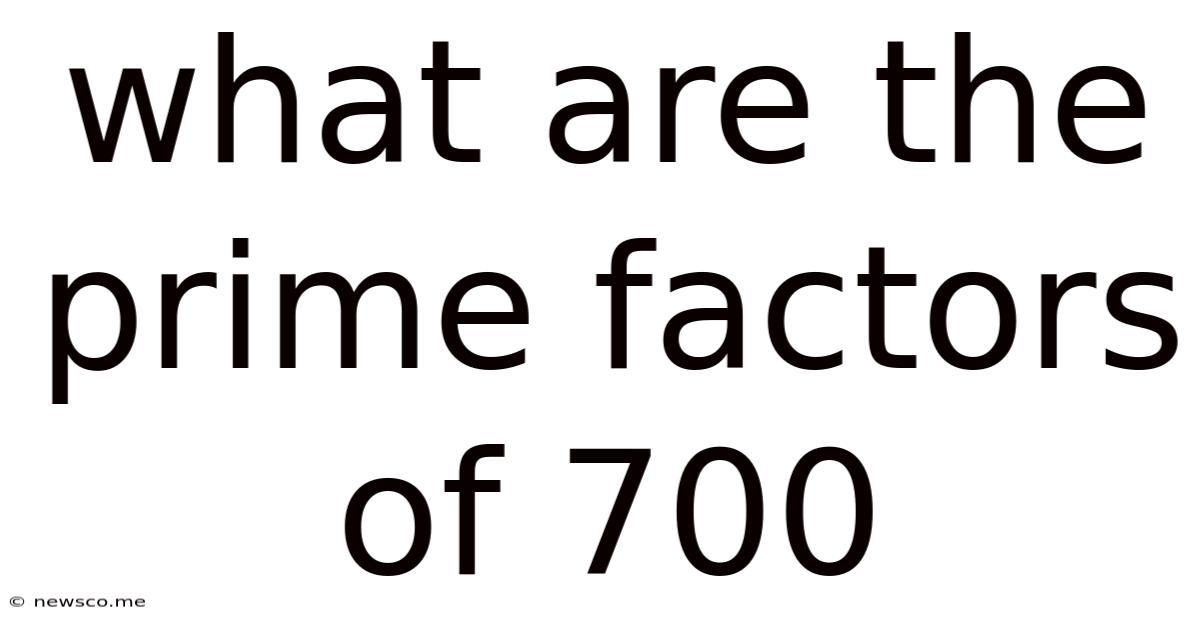
Table of Contents
What Are the Prime Factors of 700? A Deep Dive into Prime Factorization
Finding the prime factors of a number might seem like a simple mathematical exercise, but understanding the process unlocks a deeper understanding of number theory and its applications. This article will explore the prime factorization of 700, explaining the method step-by-step and delving into the broader significance of prime numbers and their factorization.
Understanding Prime Numbers and Prime Factorization
Before we tackle 700, let's establish a firm foundation. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. Examples include 2, 3, 5, 7, 11, and so on. Numbers that are not prime are called composite numbers.
Prime factorization is the process of expressing a composite number as a product of its prime factors. This representation is unique for each composite number; meaning there's only one way to express it as a product of prime numbers (ignoring the order of the factors). This uniqueness is fundamental in many areas of mathematics.
Finding the Prime Factors of 700: A Step-by-Step Approach
Let's find the prime factorization of 700 using a systematic method. We'll employ the factor tree method, a visual approach that helps break down the number into its prime components.
-
Start with the smallest prime number: The smallest prime number is 2. Since 700 is an even number, it's divisible by 2.
700 = 2 x 350
-
Continue dividing by prime numbers: 350 is also even, so we can divide by 2 again:
350 = 2 x 175
-
Move to the next prime number: 175 is not divisible by 2, but it is divisible by 5 (since it ends in 5):
175 = 5 x 35
-
Keep factoring: 35 is also divisible by 5:
35 = 5 x 7
-
End with prime numbers: We've reached two prime numbers, 5 and 7. This means we've completed the factorization.
Therefore, the prime factorization of 700 is 2 x 2 x 5 x 5 x 7, which can be written more concisely as 2² x 5² x 7.
Visualizing the Process: The Factor Tree
The factor tree provides a clear visual representation of the factorization process:
700
/ \
2 350
/ \
2 175
/ \
5 35
/ \
5 7
Each branch ends in a prime number, and the product of all the prime numbers at the end of the branches equals 700.
The Significance of Prime Factorization
Prime factorization isn't just a mathematical curiosity; it has significant applications in various fields:
-
Cryptography: Prime numbers are the foundation of many modern encryption methods, such as RSA encryption, which is used to secure online transactions. The difficulty of factoring large numbers into their prime components is the key to the security of these systems.
-
Number Theory: Prime factorization is crucial for understanding fundamental concepts in number theory, such as modular arithmetic, which has applications in computer science and cryptography.
-
Computer Science: Algorithms for prime factorization are actively researched and improved, with implications for data security and computational efficiency.
-
Mathematics Education: Prime factorization helps develop critical thinking skills, problem-solving abilities, and a deeper understanding of number properties.
Beyond 700: Exploring Different Factorization Techniques
While the factor tree method is intuitive and visually appealing, other methods exist for finding prime factors:
-
Division Method: This involves systematically dividing the number by prime numbers, starting with the smallest, until only prime numbers remain. This is particularly efficient for smaller numbers.
-
Trial Division: This method involves testing for divisibility by all prime numbers up to the square root of the number. If a number has a divisor larger than its square root, it must also have a divisor smaller than its square root. This optimizes the search for factors.
-
Algorithms for Large Numbers: For extremely large numbers, specialized algorithms are employed, such as the General Number Field Sieve (GNFS), which is currently the most efficient known algorithm for factoring large numbers. These algorithms are computationally intensive and often require significant processing power.
Practical Applications and Real-World Examples
Prime factorization might seem abstract, but its principles underpin many everyday applications:
-
Simplifying Fractions: Finding the prime factors of the numerator and denominator allows for simplification of fractions to their lowest terms.
-
Finding the Least Common Multiple (LCM): Prime factorization facilitates the calculation of the LCM of two or more numbers, crucial in solving problems involving fractions and ratios.
-
Finding the Greatest Common Divisor (GCD): Similarly, prime factorization helps in determining the GCD, essential in simplifying expressions and solving various mathematical problems.
Conclusion: The Enduring Importance of Prime Numbers
The seemingly simple question of "What are the prime factors of 700?" opens the door to a vast and fascinating world of number theory and its far-reaching applications. Understanding prime factorization is not only a key element of mathematical literacy but also a cornerstone of modern cryptography and computer science. Whether you're simplifying fractions, securing online transactions, or exploring the intricacies of number theory, prime numbers and their factorization remain essential concepts. The ability to efficiently and accurately find the prime factors of a number is a valuable skill with implications far beyond the classroom. So, remember the prime factorization of 700 (2² x 5² x 7) – it's a small example with a big impact.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Are The Prime Factors Of 700 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.