What Are The Prime Factors Of 735
News Co
Mar 25, 2025 · 4 min read
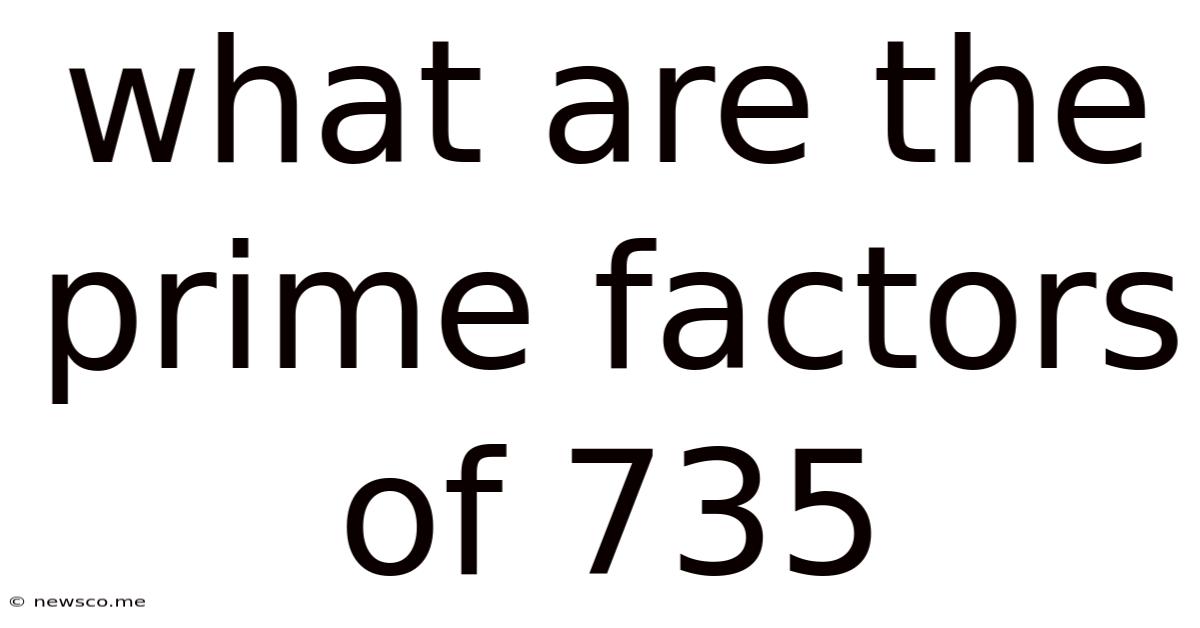
Table of Contents
What are the Prime Factors of 735? A Deep Dive into Prime Factorization
Finding the prime factors of a number might seem like a simple mathematical exercise, but it's a fundamental concept in number theory with applications far beyond the classroom. Understanding prime factorization is crucial for various mathematical operations, from simplifying fractions to solving complex equations. This article will delve into the process of finding the prime factors of 735, explaining the method step-by-step and exploring the broader significance of prime numbers and factorization.
Understanding Prime Numbers and Prime Factorization
Before we tackle 735, let's clarify some key terms. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. Examples include 2, 3, 5, 7, 11, and so on. A number that is not prime is called a composite number.
Prime factorization is the process of breaking down a composite number into its prime number components. Every composite number can be uniquely expressed as a product of prime numbers. This unique representation is known as the fundamental theorem of arithmetic.
Finding the Prime Factors of 735: A Step-by-Step Approach
Now, let's find the prime factors of 735. We'll use a method that involves repeatedly dividing by the smallest prime number possible until we're left with only prime numbers.
-
Start with the smallest prime number, 2: 735 is an odd number, so it's not divisible by 2.
-
Try the next prime number, 3: The sum of the digits of 735 (7 + 3 + 5 = 15) is divisible by 3, therefore 735 is divisible by 3. 735 / 3 = 245.
-
Continue with 3: 245 is also divisible by 5. 245 / 5 = 49
-
Try the next prime number, 5: This time, we found that 49 is not divisible by 5.
-
Try the next prime number, 7: 49 is divisible by 7. 49 / 7 = 7.
-
We're left with 7: 7 is a prime number.
Therefore, the prime factorization of 735 is 3 x 5 x 7 x 7, which can also be written as 3 x 5 x 7².
Visualizing Prime Factorization: Factor Trees
A helpful visual aid for prime factorization is a factor tree. Here's how a factor tree for 735 would look:
735
/ \
3 245
/ \
5 49
/ \
7 7
This tree clearly shows the branching process of finding the prime factors until we reach only prime numbers at the ends of the branches.
Applications of Prime Factorization
The seemingly simple process of prime factorization has far-reaching applications in various areas of mathematics and beyond:
-
Simplifying Fractions: Finding the greatest common divisor (GCD) of the numerator and denominator of a fraction is crucial for simplification. Prime factorization makes finding the GCD straightforward. For example, simplifying the fraction 735/1050 would be much easier after finding the prime factors of both numbers.
-
Solving Diophantine Equations: These are equations where only integer solutions are sought. Prime factorization often plays a vital role in solving these types of equations.
-
Cryptography: Prime numbers are fundamental to many modern encryption techniques, like RSA encryption. The security of these systems relies on the difficulty of factoring very large numbers into their prime components.
-
Modular Arithmetic: Used extensively in computer science and cryptography, modular arithmetic relies heavily on prime numbers and their properties.
-
Finding Least Common Multiple (LCM): Similar to finding the GCD, the LCM of two or more numbers is easily calculated using prime factorization.
Beyond 735: Exploring Prime Factorization Techniques
While the method we used for 735 is effective for smaller numbers, larger numbers require more sophisticated techniques. Here are some approaches for factoring larger numbers:
-
Trial Division: This is the most basic method, testing divisibility by successive prime numbers. It becomes inefficient for very large numbers.
-
Pollard's Rho Algorithm: A probabilistic algorithm that is more efficient than trial division for factoring larger numbers.
-
Quadratic Sieve: A more advanced algorithm for factoring large composite numbers, used in breaking certain types of encryption.
-
General Number Field Sieve (GNFS): Currently the fastest known algorithm for factoring extremely large numbers.
The Significance of Prime Numbers in Mathematics
Prime numbers are considered the building blocks of all other whole numbers. Their distribution is a subject of ongoing research, and many unsolved problems in number theory relate to prime numbers. Some notable examples include:
-
The Twin Prime Conjecture: This conjecture proposes that there are infinitely many pairs of prime numbers that differ by 2 (e.g., 3 and 5, 11 and 13).
-
Goldbach's Conjecture: This states that every even integer greater than 2 can be expressed as the sum of two primes.
-
Riemann Hypothesis: This is one of the most important unsolved problems in mathematics, relating to the distribution of prime numbers.
Conclusion: The Enduring Importance of Prime Factors
The seemingly simple act of finding the prime factors of 735 – 3 x 5 x 7² – reveals a deeper connection to fundamental concepts in number theory. Understanding prime factorization is not just about solving mathematical problems; it unlocks the ability to appreciate the underlying structure of numbers and their importance in various fields, from cryptography to computer science. The quest to understand prime numbers continues to drive mathematical research and technological innovation, highlighting their enduring importance in the world of numbers.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Are The Prime Factors Of 735 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.