What Are The Prime Factors Of 92
News Co
Apr 07, 2025 · 5 min read
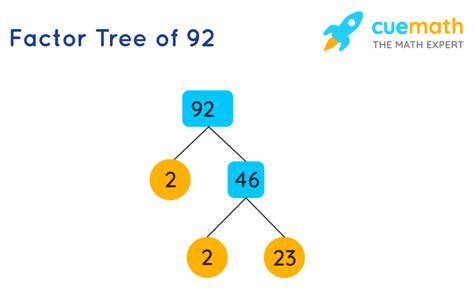
Table of Contents
What Are the Prime Factors of 92? A Deep Dive into Prime Factorization
The seemingly simple question, "What are the prime factors of 92?" opens a door to a fascinating branch of mathematics: number theory. While the answer itself is straightforward, exploring the process of prime factorization reveals fundamental concepts crucial to understanding more complex mathematical ideas. This article will not only answer the question but delve into the underlying principles, providing a comprehensive understanding of prime numbers, prime factorization, and its applications.
Understanding Prime Numbers
Before we tackle the prime factors of 92, let's solidify our understanding of prime numbers. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. In simpler terms, it's only divisible by 1 and itself without leaving a remainder. The first few prime numbers are 2, 3, 5, 7, 11, 13, and so on. The number 1 is not considered a prime number.
It's important to note that the concept of prime numbers is fundamental to number theory. They are the building blocks of all other natural numbers, much like atoms are the building blocks of matter. This is the essence of prime factorization.
Identifying Prime Numbers: A Quick Guide
While determining whether a very large number is prime can be computationally intensive, smaller numbers can be checked relatively easily. The most basic method involves systematically checking for divisibility by potential prime factors. For example, to check if 17 is prime, we would test divisibility by 2, 3, 5, 7, 11, and 13 (since the square root of 17 is approximately 4.12). If none of these numbers divide 17 evenly, then 17 is a prime number. More sophisticated algorithms exist for larger numbers, but this method suffices for our current purpose.
Prime Factorization: Breaking Down Numbers
Prime factorization is the process of expressing a composite number (a number that is not prime) as a product of its prime factors. Each composite number can be uniquely expressed as a product of primes, regardless of the order of the factors. This uniqueness is a cornerstone of number theory and is known as the Fundamental Theorem of Arithmetic.
For example, let's factorize the number 12:
12 = 2 x 6
12 = 2 x 2 x 3
Notice that regardless of our initial approach, we end up with the same prime factors: 2, 2, and 3. We can represent this concisely as 2² x 3. This is the prime factorization of 12.
Finding the Prime Factors of 92
Now, let's apply the process of prime factorization to 92. We start by finding the smallest prime number that divides 92. That's 2:
92 = 2 x 46
Now, we continue the process with 46. Again, 2 is the smallest prime factor:
46 = 2 x 23
23 is a prime number. Therefore, the prime factorization of 92 is:
92 = 2 x 2 x 23 = 2² x 23
Therefore, the prime factors of 92 are 2 and 23.
Applications of Prime Factorization
Prime factorization, although seemingly a simple mathematical exercise, has significant applications across various fields:
1. Cryptography: Securing Online Transactions
Prime numbers play a crucial role in modern cryptography. Algorithms like RSA (Rivest-Shamir-Adleman) rely on the difficulty of factoring extremely large numbers into their prime factors. The security of online transactions, secure communication protocols, and digital signatures heavily depend on this computational challenge.
2. Modular Arithmetic and Number Theory: Advanced Mathematical Concepts
Prime factorization is fundamental to many concepts in modular arithmetic and abstract algebra. Understanding prime factors is essential for studying congruences, Fermat's Little Theorem, and other significant theorems in number theory.
3. Coding Theory: Error Detection and Correction
Prime numbers are used in the design of error-correcting codes. These codes are vital for ensuring reliable data transmission and storage, especially in situations where noise or interference might corrupt the data.
4. Computer Science: Algorithm Design and Analysis
The efficiency of algorithms often depends on the properties of prime numbers. For example, certain algorithms for primality testing or factorization have performance characteristics directly related to the distribution of prime numbers.
Exploring Further: Methods for Prime Factorization
While we used a simple method to factorize 92, larger numbers require more efficient algorithms. Here are a few commonly used techniques:
-
Trial Division: This is the most basic method, as demonstrated above. It involves systematically trying to divide the number by each prime number, starting from 2.
-
Sieve of Eratosthenes: This is a more efficient algorithm for generating a list of prime numbers up to a given limit. It's not directly a factorization algorithm, but it provides a readily available list of potential prime factors to test.
-
Pollard's Rho Algorithm: This is a probabilistic algorithm that is particularly efficient for factoring numbers with small prime factors.
-
General Number Field Sieve (GNFS): This is the most efficient known algorithm for factoring very large numbers, currently used for breaking RSA encryption with large keys.
Conclusion: The Significance of Prime Factors
The seemingly simple question of the prime factors of 92 – which are 2 and 23 – leads us into a rich and complex area of mathematics. Understanding prime factorization provides insights into the fundamental building blocks of numbers, underpins sophisticated cryptographic techniques, and has broad applications across multiple fields. From securing our online transactions to designing efficient algorithms, the concept of prime factors proves its relevance and power. The seemingly simple process of finding the prime factors of 92 is, therefore, a gateway to understanding a vast and fascinating realm of mathematical inquiry.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Are The Prime Factors Of 92 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.