What Are The Roots Of Y X2 3x 10
News Co
Apr 22, 2025 · 5 min read
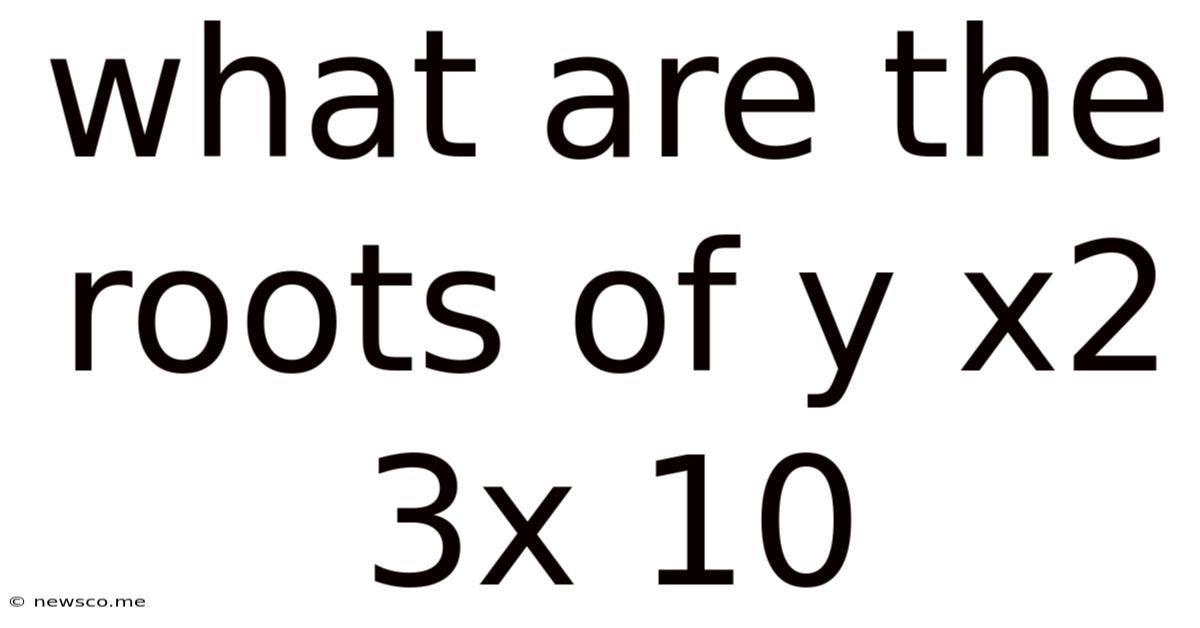
Table of Contents
What Are the Roots of y = x² + 3x - 10? A Deep Dive into Quadratic Equations
Finding the roots (or zeros) of a quadratic equation is a fundamental concept in algebra. Understanding how to solve these equations opens doors to numerous applications in various fields, from physics and engineering to economics and computer science. This article will explore the various methods of finding the roots of the quadratic equation y = x² + 3x - 10, offering a comprehensive understanding of the underlying principles and demonstrating practical solutions.
Understanding Quadratic Equations and Their Roots
A quadratic equation is an equation of the form ax² + bx + c = 0, where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero. The roots of a quadratic equation are the values of 'x' that satisfy the equation, meaning they make the equation true. Graphically, these roots represent the x-intercepts of the parabola defined by the quadratic function. Our specific equation, y = x² + 3x - 10, is a quadratic equation where a = 1, b = 3, and c = -10. Finding the roots means determining the x-values where y = 0.
Why Finding Roots Matters
The roots of a quadratic equation provide crucial information about the behavior of the function it represents. They reveal:
- X-intercepts: As mentioned, they pinpoint where the parabola intersects the x-axis.
- Solutions to Problems: In real-world applications, the roots often represent solutions to problems involving projectile motion, area calculations, optimization, and more.
- Factors: The roots help us factor the quadratic expression, which simplifies further algebraic manipulations.
Methods for Finding the Roots
Several methods exist for solving quadratic equations. We'll explore the three most common: factoring, the quadratic formula, and completing the square.
1. Factoring
Factoring is a powerful method when the quadratic expression can be easily factored. It involves expressing the quadratic as a product of two linear expressions. For our equation, y = x² + 3x - 10, we look for two numbers that add up to 3 (the coefficient of x) and multiply to -10 (the constant term). These numbers are 5 and -2. Therefore, we can factor the equation as:
(x + 5)(x - 2) = 0
To find the roots, we set each factor equal to zero and solve:
- x + 5 = 0 => x = -5
- x - 2 = 0 => x = 2
Therefore, the roots of the equation y = x² + 3x - 10 are x = -5 and x = 2.
2. The Quadratic Formula
The quadratic formula is a general method that works for all quadratic equations, regardless of whether they can be easily factored. The formula is derived by completing the square for the general quadratic equation ax² + bx + c = 0 and is given by:
x = [-b ± √(b² - 4ac)] / 2a
For our equation, a = 1, b = 3, and c = -10. Substituting these values into the quadratic formula, we get:
x = [-3 ± √(3² - 4 * 1 * -10)] / (2 * 1) x = [-3 ± √(9 + 40)] / 2 x = [-3 ± √49] / 2 x = [-3 ± 7] / 2
This gives us two solutions:
- x = (-3 + 7) / 2 = 2
- x = (-3 - 7) / 2 = -5
Again, we find the roots to be x = 2 and x = -5.
3. Completing the Square
Completing the square is a method that involves manipulating the quadratic equation to create a perfect square trinomial. This method is particularly useful when the quadratic cannot be easily factored or when dealing with equations in other forms.
To complete the square for y = x² + 3x - 10, we follow these steps:
- Move the constant term to the right side: x² + 3x = 10
- Take half of the coefficient of x (3/2), square it ((3/2)² = 9/4), and add it to both sides: x² + 3x + 9/4 = 10 + 9/4
- Factor the left side as a perfect square: (x + 3/2)² = 49/4
- Take the square root of both sides: x + 3/2 = ±7/2
- Solve for x:
- x = -3/2 + 7/2 = 2
- x = -3/2 - 7/2 = -5
Once again, the roots are x = 2 and x = -5.
Comparing the Methods
Each method has its advantages and disadvantages:
- Factoring: Easiest and fastest when applicable but not always possible.
- Quadratic Formula: Always works, but can be more time-consuming.
- Completing the Square: Useful for specific applications and for deriving the quadratic formula, but can be cumbersome for some equations.
The Discriminant and the Nature of Roots
The expression b² - 4ac within the quadratic formula is called the discriminant. It provides valuable information about the nature of the roots:
- b² - 4ac > 0: Two distinct real roots (as in our example).
- b² - 4ac = 0: One real root (a repeated root).
- b² - 4ac < 0: Two complex roots (involving imaginary numbers).
In our case, the discriminant is 3² - 4(1)(-10) = 49, which is greater than 0, confirming that we have two distinct real roots.
Applications of Quadratic Equations
The ability to find the roots of quadratic equations is essential in a wide variety of fields:
- Physics: Projectile motion, calculating the trajectory of objects under gravity.
- Engineering: Designing structures, optimizing shapes and sizes.
- Economics: Modeling supply and demand, maximizing profits.
- Computer Graphics: Creating curves and shapes.
- Data Analysis: Curve fitting and modeling trends.
Conclusion
Finding the roots of the quadratic equation y = x² + 3x - 10 is a fundamental skill in algebra with far-reaching applications. Whether you use factoring, the quadratic formula, or completing the square, understanding the underlying principles and choosing the most appropriate method is crucial for success in various mathematical and real-world problems. The discriminant provides additional insight into the nature of the roots, enhancing our understanding of the behavior of quadratic functions. Mastering these techniques empowers you to tackle more complex mathematical challenges and opens doors to a deeper comprehension of the world around us.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Are The Roots Of Y X2 3x 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.