What Are The Solutions Of X2 8 5x
News Co
May 09, 2025 · 5 min read
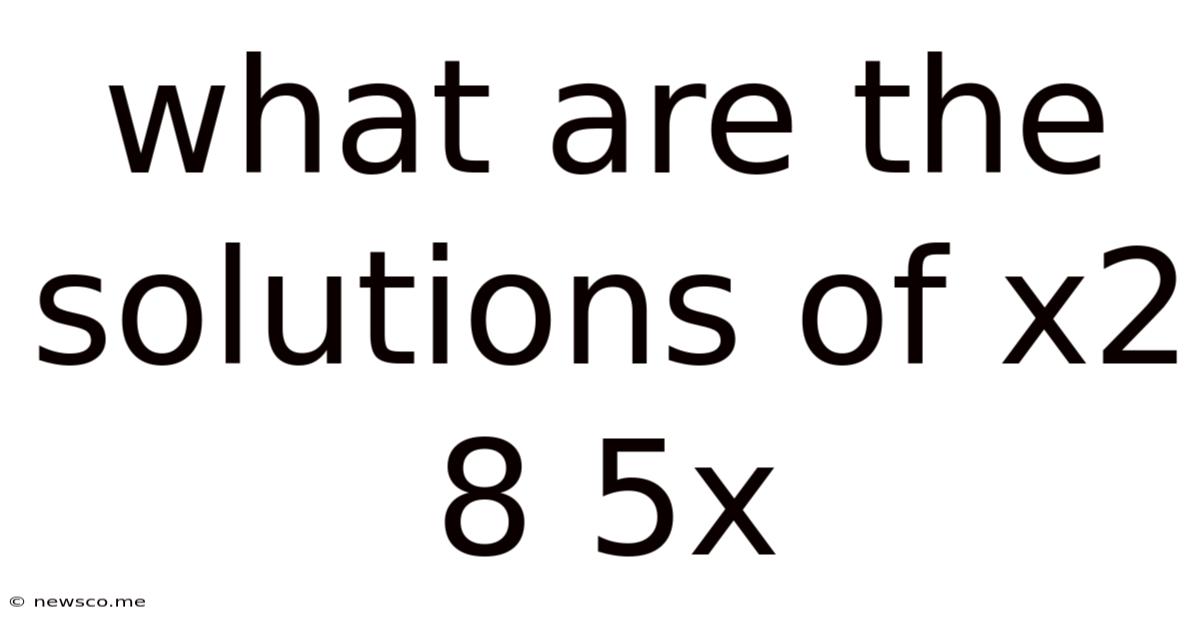
Table of Contents
Solving the Quadratic Equation: x² + 5x - 8 = 0
The quadratic equation x² + 5x - 8 = 0 is a common problem encountered in algebra. Understanding how to solve this type of equation is crucial for various applications in mathematics, science, and engineering. This comprehensive guide will explore multiple methods for solving this specific equation and provide a broader understanding of solving quadratic equations in general. We'll delve into the intricacies of each method, ensuring you gain a solid grasp of the underlying concepts.
Understanding Quadratic Equations
Before diving into the solutions, let's establish a foundational understanding of quadratic equations. A quadratic equation is an equation of the form ax² + bx + c = 0, where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero. In our case, a = 1, b = 5, and c = -8. The solutions to a quadratic equation are also known as its roots or zeros. These represent the x-values where the quadratic function intersects the x-axis.
Method 1: Quadratic Formula
The quadratic formula is a powerful tool that provides a direct solution for any quadratic equation. The formula is derived from completing the square and is universally applicable. The formula is:
x = (-b ± √(b² - 4ac)) / 2a
Let's apply this formula to our equation:
x² + 5x - 8 = 0
Here, a = 1, b = 5, and c = -8. Substituting these values into the quadratic formula, we get:
x = (-5 ± √(5² - 4 * 1 * -8)) / (2 * 1) x = (-5 ± √(25 + 32)) / 2 x = (-5 ± √57) / 2
Therefore, the two solutions are:
- x = (-5 + √57) / 2 ≈ 1.2749
- x = (-5 - √57) / 2 ≈ -6.2749
The quadratic formula provides an exact solution, even when the roots are irrational, as in this case. This makes it a reliable and widely used method.
Method 2: Completing the Square
Completing the square is another algebraic technique used to solve quadratic equations. This method involves manipulating the equation to create a perfect square trinomial, which can then be easily factored. Let's demonstrate this process:
-
Move the constant term to the right side:
x² + 5x = 8
-
Take half of the coefficient of x (which is 5), square it ((5/2)² = 6.25), and add it to both sides:
x² + 5x + 6.25 = 8 + 6.25 x² + 5x + 6.25 = 14.25
-
Factor the left side as a perfect square trinomial:
(x + 2.5)² = 14.25
-
Take the square root of both sides:
x + 2.5 = ±√14.25
-
Solve for x:
x = -2.5 ± √14.25 x ≈ -2.5 ± 3.7749
Therefore, the two solutions are:
- x ≈ 1.2749
- x ≈ -6.2749
These solutions are consistent with those obtained using the quadratic formula. Completing the square is a valuable technique that enhances understanding of quadratic equations and their geometric representation.
Method 3: Factoring (Not Directly Applicable)
Factoring is a straightforward method for solving quadratic equations when the equation can be easily factored into two linear expressions. However, in our case, x² + 5x - 8 = 0 doesn't factor neatly using integers. We would need to use irrational numbers or approximate values to factor, making this method less efficient for this particular equation. While factoring is efficient for certain quadratic equations, it's not always applicable.
Method 4: Graphical Method
The graphical method provides a visual representation of the solutions. By plotting the quadratic function y = x² + 5x - 8, the x-intercepts of the graph represent the solutions to the equation. Using graphing software or a calculator, we can plot the function and observe where the parabola intersects the x-axis. The x-coordinates of these intersection points correspond to the solutions.
While this method provides a visual understanding, it relies on the accuracy of the graph and might not always yield precise solutions, especially if the roots are irrational. However, it's helpful for visualizing the behavior of the quadratic function and understanding the concept of roots.
Discriminant and Nature of Roots
The expression within the square root in the quadratic formula (b² - 4ac) is known as the discriminant. The discriminant determines the nature of the roots:
- b² - 4ac > 0: Two distinct real roots (as in our case)
- b² - 4ac = 0: One real root (a repeated root)
- b² - 4ac < 0: Two complex conjugate roots (involving imaginary numbers)
In our equation, the discriminant is 5² - 4 * 1 * -8 = 57, which is positive. This confirms that the equation has two distinct real roots.
Applications of Quadratic Equations
Quadratic equations have wide-ranging applications across numerous fields:
- Physics: Calculating projectile motion, determining the trajectory of objects under gravity.
- Engineering: Designing structures, analyzing electrical circuits, modeling oscillations.
- Economics: Optimizing production, analyzing market trends, modeling growth.
- Computer Graphics: Creating curves and shapes.
Understanding how to solve quadratic equations is essential for tackling problems in these and many other areas.
Conclusion
Solving the quadratic equation x² + 5x - 8 = 0 can be achieved through various methods, each with its advantages and limitations. The quadratic formula provides a universal and precise solution, while completing the square offers an algebraic approach that enhances understanding. The graphical method provides a visual representation. Understanding the discriminant helps predict the nature of the solutions. Mastering these techniques is crucial for success in mathematics and its applications in various disciplines. By understanding the core concepts and applying the appropriate methods, one can effectively solve a wide range of quadratic equations. This detailed explanation empowers you to tackle similar problems with confidence and build a stronger foundation in algebra. Remember to practice regularly to reinforce your understanding and improve your problem-solving skills.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Are The Solutions Of X2 8 5x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.