What Are The Square Roots Of 196
News Co
Mar 25, 2025 · 5 min read
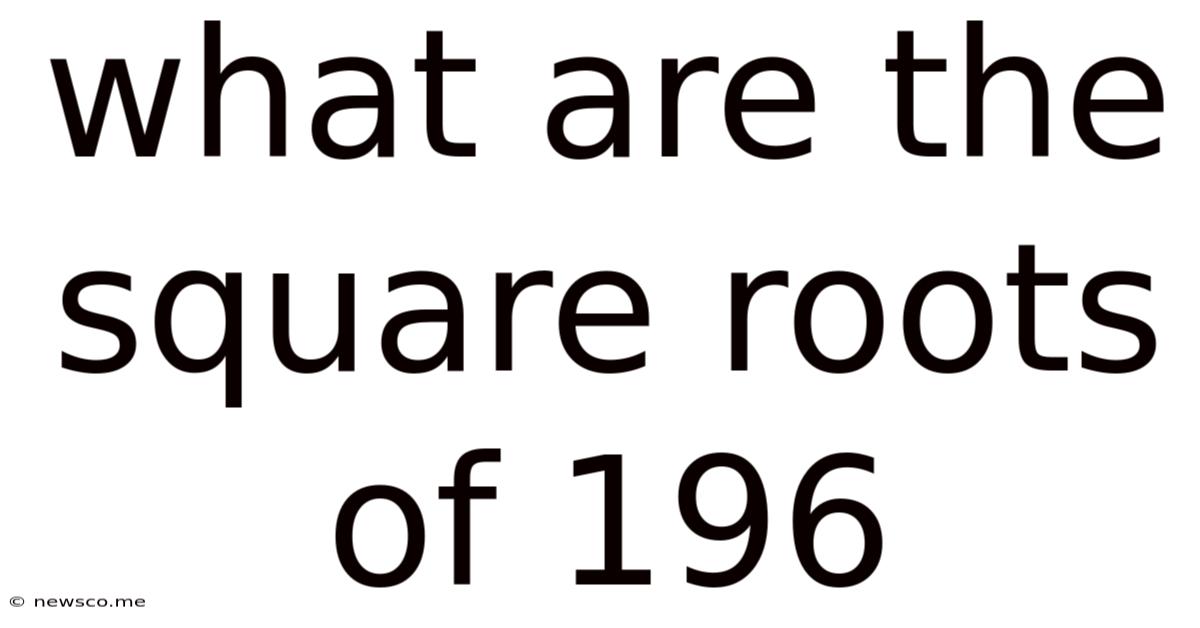
Table of Contents
What are the Square Roots of 196? A Deep Dive into Square Roots and Their Applications
Finding the square root of a number is a fundamental concept in mathematics, with applications spanning various fields. This article delves into the question, "What are the square roots of 196?", exploring the concept of square roots, different methods for calculating them, and the practical significance of understanding this mathematical operation. We'll also touch upon related concepts and explore more advanced applications.
Understanding Square Roots
Before we tackle the specific problem of finding the square roots of 196, let's establish a solid understanding of what a square root actually is.
A square root of a number x is a value that, when multiplied by itself, gives x. In other words, if y is the square root of x, then y × y = x. This is often represented mathematically as √x = y.
Important Note: Every positive number has two square roots: a positive square root and a negative square root. For example, the square roots of 25 are +5 and -5, because 5 × 5 = 25 and (-5) × (-5) = 25. The symbol √ typically represents the principal square root, which is the non-negative square root.
Calculating the Square Roots of 196
Now, let's focus on finding the square roots of 196. There are several ways to approach this:
1. Prime Factorization Method
This method involves breaking down the number into its prime factors. Prime factorization is the process of expressing a number as a product of prime numbers.
-
Find the prime factors of 196: 196 = 2 × 98 = 2 × 2 × 49 = 2 × 2 × 7 × 7 = 2² × 7²
-
Take the square root: √196 = √(2² × 7²) = √2² × √7² = 2 × 7 = 14
Therefore, the principal square root of 196 is 14. Since we know every positive number has two square roots, the other square root is -14. So, the square roots of 196 are 14 and -14.
2. Using a Calculator
The simplest method is to use a calculator. Most calculators have a square root function (√) that directly provides the principal square root. Inputting 196 into the square root function will yield 14. Remember to consider both the positive and negative square roots.
3. Perfect Squares Recognition
This method relies on recognizing perfect squares. A perfect square is a number that is the square of an integer. Through practice and familiarity, you can quickly identify perfect squares. Since 14 × 14 = 196, we can directly identify 14 as the principal square root.
Applications of Square Roots
Understanding square roots is crucial in numerous mathematical and real-world applications:
1. Geometry
Square roots are fundamental in geometry for calculating distances, areas, and volumes. For instance:
-
Pythagorean Theorem: This theorem, a cornerstone of geometry, states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. Finding the length of a side often involves taking the square root.
-
Area of a Circle: The area of a circle is given by the formula A = πr², where 'r' is the radius. To find the radius given the area, you need to take the square root.
-
Volume of a Sphere: The volume of a sphere is given by the formula V = (4/3)πr³. Determining the radius from the volume again requires using square roots (after taking the cube root).
2. Physics
Square roots are frequently used in physics:
-
Velocity and Acceleration: Calculations involving velocity and acceleration often involve square roots. For example, the formula for the final velocity (v) of an object undergoing constant acceleration (a) over a distance (s) is given by v = √(u² + 2as), where 'u' is the initial velocity.
-
Energy Calculations: In physics, energy calculations frequently involve the square root of various quantities, such as kinetic energy or potential energy.
3. Engineering
Engineers use square roots extensively in various aspects of their work:
-
Structural Calculations: Engineers use square roots in structural calculations to determine stresses and strains within materials. Understanding the forces acting on structures and their resulting deformation often requires square root calculations.
-
Electrical Engineering: Square roots play a vital role in electrical engineering calculations, particularly when dealing with impedance, power, and circuit analysis.
4. Statistics
Square roots appear in statistical calculations:
-
Standard Deviation: The standard deviation, a measure of the spread or dispersion of a data set, involves taking the square root of the variance.
-
Root Mean Square (RMS): The RMS is a statistical measure used to quantify the magnitude of a varying quantity. It finds application in analyzing signals and other time-varying data.
5. Computer Graphics
Square roots are crucial in computer graphics:
-
Distance Calculations: Determining the distance between two points on a screen or in 3D space often involves the Pythagorean theorem and, consequently, square roots.
-
Vector Normalization: In computer graphics, vectors are often normalized (scaled to unit length). This process involves dividing each component of the vector by its magnitude, which is calculated using the square root of the sum of squares of its components.
Beyond the Basics: Complex Numbers
While we focused on the real square roots of 196 (14 and -14), it's worth briefly mentioning that square roots can also extend to complex numbers. Complex numbers are numbers that can be expressed in the form a + bi, where 'a' and 'b' are real numbers, and 'i' is the imaginary unit (√-1). While the square roots of 196 are real numbers, the square roots of negative numbers are complex numbers.
Conclusion
Finding the square roots of 196, while seemingly a simple task, opens the door to a deeper understanding of square roots and their widespread importance in various fields. From the fundamental concepts to the practical applications in geometry, physics, engineering, statistics, and computer graphics, understanding square roots is a crucial skill for anyone pursuing mathematical or scientific endeavors. The methods discussed, from prime factorization to calculator usage, provide versatile approaches to solving such problems. Remember to always consider both the positive and negative square roots when solving equations involving square roots, unless specified otherwise. The understanding of this fundamental mathematical concept provides a solid foundation for more advanced mathematical studies.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Are The Square Roots Of 196 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.