What Factors Do 18 And 30 Have In Common
News Co
Apr 02, 2025 · 5 min read
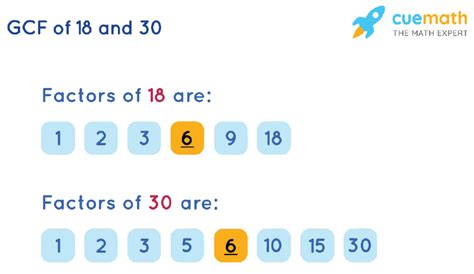
Table of Contents
What Factors Do 18 and 30 Have in Common? A Deep Dive into Number Theory
The seemingly simple question, "What factors do 18 and 30 have in common?" opens a door to a fascinating exploration of number theory, prime factorization, and the relationships between integers. While the immediate answer might seem straightforward, a deeper investigation reveals a richer understanding of mathematical concepts and their applications. This article will delve into the shared factors of 18 and 30, exploring their prime factorizations, greatest common divisors (GCD), least common multiples (LCM), and the broader implications of these concepts in mathematics and beyond.
Understanding Factors and Prime Factorization
Before we dive into the specifics of 18 and 30, let's establish a firm foundation. A factor (or divisor) of a number is an integer that divides the number evenly without leaving a remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12.
Prime factorization is the process of expressing a number as a product of its prime factors. Prime numbers are whole numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11...). Prime factorization is unique for every number; it's like a number's "DNA."
Let's find the prime factorization of 18 and 30:
- 18: 2 x 3 x 3 = 2 x 3²
- 30: 2 x 3 x 5
Identifying Common Factors
Now we can easily identify the common factors by comparing their prime factorizations. Both 18 and 30 share the prime factors 2 and 3. Therefore, the common factors are:
- 1: Every number has 1 as a factor.
- 2: Present in both prime factorizations.
- 3: Present in both prime factorizations.
- 6: The product of the common prime factors (2 x 3).
These are all the factors that 18 and 30 have in common. Notice that we don't include 9 (a factor of 18) or 5 (a factor of 30) because they are not present in both factorizations.
The Greatest Common Divisor (GCD)
The greatest common divisor (GCD), also known as the highest common factor (HCF), is the largest number that divides both 18 and 30 without leaving a remainder. In this case, the GCD of 18 and 30 is 6. This is the largest of the common factors we identified above. The GCD is a crucial concept in various mathematical applications, including simplifying fractions and solving algebraic equations.
Several methods can calculate the GCD, including:
- Listing factors: List all factors of each number and find the largest common factor.
- Prime factorization: Find the prime factorization of each number and multiply the common prime factors raised to their lowest power. For 18 and 30, this would be 2¹ x 3¹ = 6.
- Euclidean algorithm: A more efficient algorithm for larger numbers, which involves repeated division until the remainder is zero.
The Least Common Multiple (LCM)
While the GCD focuses on the largest common divisor, the least common multiple (LCM) is the smallest positive number that is a multiple of both 18 and 30. Understanding the LCM is crucial in tasks like finding the lowest common denominator when adding fractions or determining when cyclical events will occur simultaneously.
To find the LCM of 18 and 30, we can use the following methods:
- Listing multiples: List multiples of each number until you find the smallest common multiple.
- Prime factorization: Find the prime factorization of each number and multiply the prime factors raised to their highest power. For 18 (2 x 3²) and 30 (2 x 3 x 5), the LCM would be 2¹ x 3² x 5¹ = 90.
- Formula relating GCD and LCM: There's a useful relationship between the GCD and LCM of two numbers (a and b): LCM(a, b) x GCD(a, b) = a x b. Using this formula for 18 and 30, we have: LCM(18, 30) x 6 = 18 x 30. Solving for the LCM gives us 90.
Applications Beyond Simple Arithmetic
The concepts of factors, GCD, and LCM extend far beyond basic arithmetic. They have significant applications in various fields:
- Cryptography: GCD plays a critical role in RSA encryption, a widely used public-key cryptosystem that secures online communication.
- Computer Science: GCD and LCM are used in algorithms for scheduling tasks, managing memory, and optimizing computations.
- Music Theory: The LCM is essential in understanding musical intervals and creating harmonious melodies. The relationship between different note frequencies often relies on finding common multiples.
- Engineering: GCD and LCM are applied in problems involving gear ratios, timing mechanisms, and other mechanical systems. Finding the lowest common denominator in these applications can optimize efficiency and prevent conflicts.
- Project Management: Determining when multiple projects with different durations will be completed simultaneously often involves calculating the LCM of their respective durations.
Deeper Mathematical Explorations
The seemingly simple problem of finding common factors of 18 and 30 opens doors to more advanced mathematical concepts:
- Modular Arithmetic: Understanding the remainders when numbers are divided by other numbers (modulo operation) relies on the concepts of GCD and LCM.
- Diophantine Equations: These equations involve finding integer solutions to algebraic equations. The GCD plays a crucial role in determining the solvability of these equations.
- Abstract Algebra: The concepts of GCD and LCM are generalized in abstract algebra to concepts like greatest common divisors and least common multiples of ideals in rings.
Conclusion: The Significance of Simple Numbers
The seemingly simple numbers 18 and 30, and their shared factors, provide a gateway to a vast and fascinating world of mathematical concepts. Understanding their prime factorizations, GCD, and LCM allows us to appreciate the intricate relationships between integers and their applications in diverse fields. From secure online communication to harmonious melodies, the principles explored in this analysis are fundamental to many aspects of our technological and artistic world. The next time you encounter a seemingly simple mathematical problem, remember that beneath the surface lies a rich tapestry of interconnected ideas waiting to be explored. The exploration of these fundamental mathematical concepts not only enhances our understanding of numbers but also fosters critical thinking and problem-solving skills applicable to many areas of life. The seemingly simple question of common factors reveals the depth and breadth of mathematical beauty and its power to connect seemingly disparate fields.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Factors Do 18 And 30 Have In Common . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.