What Fraction Is Equal To 4 5
News Co
Mar 16, 2025 · 5 min read
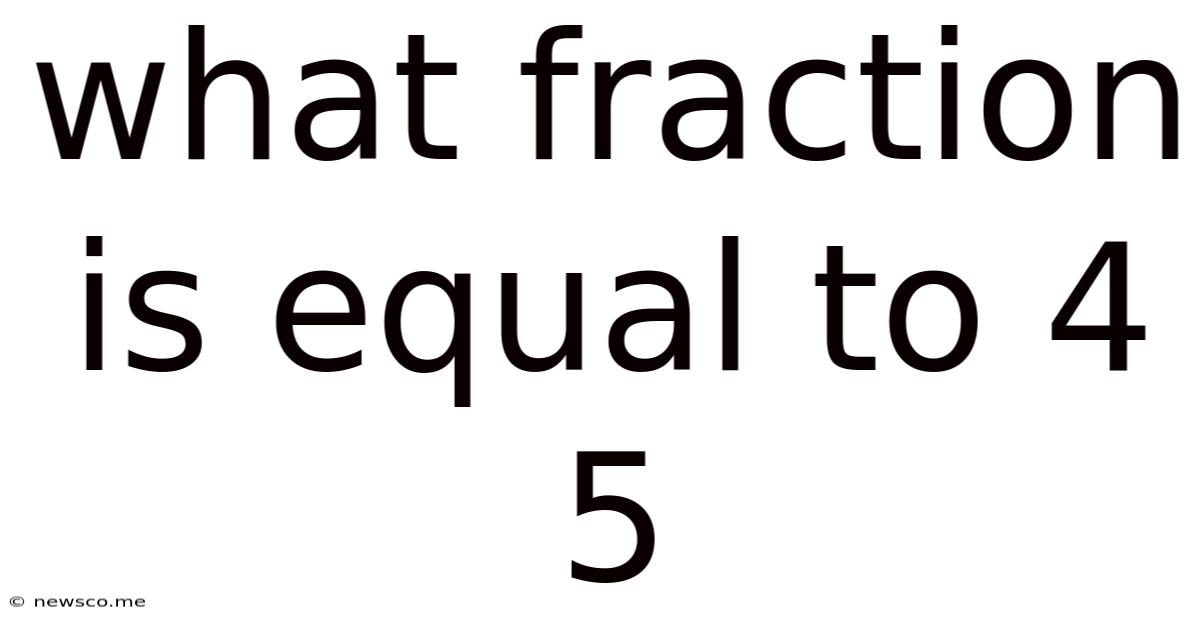
Table of Contents
What Fraction is Equal to 4/5? A Deep Dive into Fractions and Equivalents
Understanding fractions is fundamental to mathematics and numerous real-world applications. This article delves deep into the fraction 4/5, exploring its various representations, equivalent fractions, decimal form, percentage equivalent, and practical applications. We'll also touch upon related concepts to solidify your understanding of fractions.
Understanding the Fraction 4/5
The fraction 4/5 represents four parts out of a total of five equal parts. The number on top (4) is called the numerator, representing the number of parts we're considering. The number on the bottom (5) is called the denominator, indicating the total number of equal parts in the whole.
Key Characteristics of 4/5:
- Proper Fraction: The numerator (4) is smaller than the denominator (5), making it a proper fraction. Proper fractions represent a value less than one whole.
- Irreducible Fraction: 4 and 5 share no common factors other than 1. This means 4/5 is in its simplest form, also known as an irreducible fraction. It cannot be simplified further.
- Value: 4/5 represents 0.8 or 80% of a whole.
Finding Equivalent Fractions of 4/5
Equivalent fractions represent the same value but have different numerators and denominators. You can find equivalent fractions by multiplying or dividing both the numerator and the denominator by the same non-zero number. For example:
- Multiplying by 2: (4 x 2) / (5 x 2) = 8/10
- Multiplying by 3: (4 x 3) / (5 x 3) = 12/15
- Multiplying by 4: (4 x 4) / (5 x 4) = 16/20
- Multiplying by 5: (4 x 5) / (5 x 5) = 20/25
And so on. All these fractions (8/10, 12/15, 16/20, 20/25, etc.) are equivalent to 4/5. They all represent the same portion of a whole.
Conversely, you can simplify fractions to find equivalent fractions by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. Since 4/5 is already in its simplest form, we cannot simplify it further.
Identifying Equivalent Fractions
When working with fractions, it's crucial to be able to recognize equivalent fractions. This skill is fundamental for comparing fractions, adding and subtracting fractions with different denominators, and solving various mathematical problems. Practice identifying equivalent fractions will strengthen your overall fractional understanding.
4/5 as a Decimal and Percentage
Converting 4/5 to a decimal involves dividing the numerator (4) by the denominator (5):
4 ÷ 5 = 0.8
Therefore, 4/5 is equal to 0.8 as a decimal.
To convert 4/5 to a percentage, multiply the decimal equivalent by 100:
0.8 x 100 = 80%
Thus, 4/5 is equal to 80%.
Practical Applications of 4/5
The fraction 4/5 appears frequently in various real-world scenarios. Here are a few examples:
- Sales and Discounts: A store might offer an 80% (or 4/5) discount on an item.
- Surveys and Statistics: Results of a survey might indicate that 4 out of 5 people prefer a particular product.
- Measurements: A recipe might call for 4/5 of a cup of flour.
- Probabilities: The probability of a certain event occurring might be 4 out of 5.
Expanding Understanding: Related Fractional Concepts
To further solidify your understanding of fractions and 4/5, let's explore some related concepts:
Improper Fractions and Mixed Numbers
An improper fraction is a fraction where the numerator is greater than or equal to the denominator. For instance, 5/4 is an improper fraction. An improper fraction can be converted into a mixed number, which combines a whole number and a proper fraction. For example, 5/4 is equivalent to 1 ¼ (one and one-fourth). While 4/5 is a proper fraction, understanding the relationship between proper, improper fractions, and mixed numbers is crucial for comprehensive fraction knowledge.
Adding and Subtracting Fractions
Adding and subtracting fractions requires a common denominator. If the fractions have the same denominator, you simply add or subtract the numerators. If they have different denominators, you must find a common denominator before performing the operation. For example, adding 4/5 and 1/5 is straightforward: 4/5 + 1/5 = 5/5 = 1. However, adding 4/5 and 1/2 requires finding a common denominator (10): 8/10 + 5/10 = 13/10 = 1 3/10.
Multiplying and Dividing Fractions
Multiplying fractions involves multiplying the numerators and multiplying the denominators. For example, (4/5) x (1/2) = 4/10 = 2/5. Dividing fractions involves inverting the second fraction (reciprocal) and then multiplying. For example, (4/5) ÷ (1/2) = (4/5) x (2/1) = 8/5 = 1 3/5.
Comparing Fractions
Comparing fractions requires finding a common denominator or converting them to decimals. For example, to compare 4/5 and 3/4, you could find a common denominator of 20: 16/20 and 15/20. Since 16/20 > 15/20, 4/5 > 3/4. Alternatively, you could convert them to decimals: 4/5 = 0.8 and 3/4 = 0.75. Again, 0.8 > 0.75.
Conclusion: Mastering Fractions
Understanding the fraction 4/5, its equivalents, and related concepts is vital for success in mathematics and many real-world applications. Mastering fractions builds a strong foundation for more advanced mathematical concepts. Through practice and consistent application, you can develop a deep understanding and confidently handle fractions in any context. Remember to practice regularly, explore different problems, and don't hesitate to seek clarification when needed. The more you work with fractions, the easier they become!
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Fraction Is Equal To 4 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.