What Fraction Is Equivalent To 4 5
News Co
Apr 05, 2025 · 5 min read
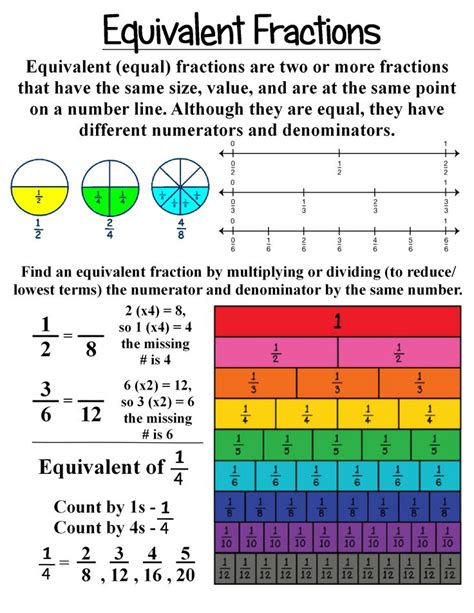
Table of Contents
What Fraction is Equivalent to 4/5? A Deep Dive into Equivalent Fractions
Understanding equivalent fractions is a fundamental concept in mathematics, crucial for various applications from simple arithmetic to advanced calculus. This article will explore the concept of equivalent fractions, focusing specifically on fractions equivalent to 4/5. We'll delve into the methods for finding them, their practical applications, and offer plenty of examples to solidify your understanding.
Understanding Equivalent Fractions
Equivalent fractions represent the same proportion or value, even though they appear different. Imagine slicing a pizza: one-half (1/2) is the same as two-quarters (2/4) or four-eighths (4/8). These fractions, despite their different numerators and denominators, represent the same amount of pizza. The key is the relationship between the numerator (the top number) and the denominator (the bottom number).
The Fundamental Principle: To find an equivalent fraction, you must multiply or divide both the numerator and the denominator by the same non-zero number. This ensures you maintain the original proportion.
Finding Equivalent Fractions for 4/5
Let's apply this principle to find equivalent fractions for 4/5. We can create an infinite number of equivalent fractions by multiplying both the numerator and denominator by any non-zero integer.
Examples:
- Multiplying by 2: (4 x 2) / (5 x 2) = 8/10
- Multiplying by 3: (4 x 3) / (5 x 3) = 12/15
- Multiplying by 4: (4 x 4) / (5 x 4) = 16/20
- Multiplying by 5: (4 x 5) / (5 x 5) = 20/25
- Multiplying by 10: (4 x 10) / (5 x 10) = 40/50
- Multiplying by 100: (4 x 100) / (5 x 100) = 400/500
And so on... You can continue this process indefinitely, generating an endless series of equivalent fractions.
Simplifying Fractions: The Reverse Process
The opposite of finding equivalent fractions by multiplying is simplifying them by dividing. This involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. The GCD is the largest number that divides both the numerator and denominator without leaving a remainder.
Let's consider some fractions equivalent to 4/5 and simplify them back to the original:
- 8/10: The GCD of 8 and 10 is 2. Dividing both by 2 gives 4/5.
- 12/15: The GCD of 12 and 15 is 3. Dividing both by 3 gives 4/5.
- 16/20: The GCD of 16 and 20 is 4. Dividing both by 4 gives 4/5.
- 20/25: The GCD of 20 and 25 is 5. Dividing both by 5 gives 4/5.
Practical Applications of Equivalent Fractions
Understanding equivalent fractions is crucial in various mathematical contexts and real-world scenarios:
1. Comparing Fractions:
When comparing fractions with different denominators, finding equivalent fractions with a common denominator makes the comparison straightforward. For example, comparing 4/5 and 3/4 would involve finding equivalent fractions with a common denominator (e.g., 20). 4/5 becomes 16/20, and 3/4 becomes 15/20. This clearly shows that 4/5 is greater than 3/4.
2. Addition and Subtraction of Fractions:
Adding or subtracting fractions requires a common denominator. Equivalent fractions are essential for finding this common denominator and performing the operation.
3. Ratio and Proportion:
Equivalent fractions are fundamental to understanding ratios and proportions. A ratio of 4:5 is the same as 8:10, 12:15, and so on. These ratios, expressed as fractions (4/5, 8/10, 12/15), represent equivalent fractions.
4. Scaling and Measurement:
In various fields like cooking, construction, and engineering, scaling requires working with equivalent fractions. For instance, if a recipe calls for 4/5 of a cup of flour, you could use equivalent fractions like 8/10 or 16/20 of a cup to achieve the same result.
5. Percentage Calculations:
Converting fractions to percentages involves finding an equivalent fraction with a denominator of 100. For 4/5, this would be 80/100, which is equivalent to 80%.
Visualizing Equivalent Fractions
Visual representations can help solidify the understanding of equivalent fractions. Imagine a rectangle divided into five equal parts, with four shaded. This visually represents 4/5. Now, imagine dividing each of the five parts in half. You now have ten parts, with eight shaded. This visually demonstrates that 4/5 is equivalent to 8/10. Similar visual representations can be used to demonstrate other equivalent fractions.
Beyond Simple Multiplication and Division: Finding Equivalent Fractions through Prime Factorization
A more advanced method for finding equivalent fractions involves prime factorization. This method is particularly useful for finding the simplest form of a fraction (reducing to lowest terms) or for finding a common denominator when adding or subtracting fractions.
Steps:
-
Find the prime factorization of the numerator and denominator. Prime factorization means expressing a number as the product of its prime factors (numbers divisible only by 1 and themselves).
-
Identify common factors. Look for prime factors that are common to both the numerator and the denominator.
-
Simplify by cancelling common factors. Divide both the numerator and denominator by the common factors. This process leaves you with the simplest form of the fraction.
Example: Let's simplify 20/25 using prime factorization.
-
Prime factorization: 20 = 2 x 2 x 5; 25 = 5 x 5
-
Common factor: 5 is a common factor.
-
Simplification: (2 x 2 x 5) / (5 x 5) = (2 x 2) / 5 = 4/5
Conclusion: Mastering Equivalent Fractions
Understanding and manipulating equivalent fractions is a cornerstone of mathematical proficiency. This comprehensive guide has covered various methods for finding equivalent fractions for 4/5, emphasizing the importance of the fundamental principle of multiplying or dividing both the numerator and denominator by the same non-zero number. We've explored practical applications, and visual and advanced methods, ensuring a solid understanding of this vital concept. By mastering equivalent fractions, you lay the foundation for more advanced mathematical concepts and confidently tackle various real-world problems. Remember to practice regularly to build fluency and reinforce your knowledge.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Fraction Is Equivalent To 4 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.