What Fractions Are Equivalent To 1/4
News Co
Mar 20, 2025 · 6 min read
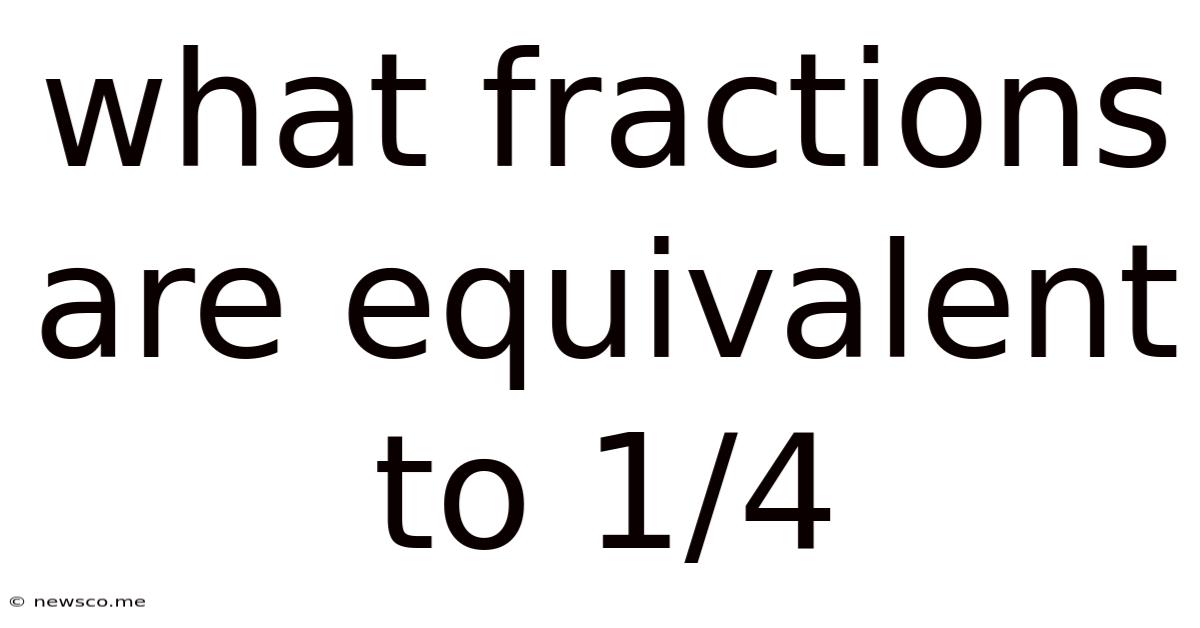
Table of Contents
What Fractions Are Equivalent to 1/4? A Comprehensive Guide
Understanding equivalent fractions is a fundamental concept in mathematics, crucial for mastering arithmetic, algebra, and beyond. This comprehensive guide delves deep into the world of fractions equivalent to 1/4, exploring various methods to identify them, their practical applications, and how to confidently work with them in different mathematical contexts.
Understanding Equivalent Fractions
Before we dive into the specifics of fractions equivalent to 1/4, let's establish a solid foundation. Equivalent fractions represent the same proportion or value, even though they appear different. Think of it like slicing a pizza: one-half (1/2) of a pizza is the same amount as two-quarters (2/4) or four-eighths (4/8), even though the number of slices differs. The key is the ratio remains constant.
The core principle behind equivalent fractions is the concept of multiplying or dividing both the numerator (top number) and the denominator (bottom number) by the same non-zero number. This operation maintains the proportional relationship, resulting in an equivalent fraction.
Finding Fractions Equivalent to 1/4
There are infinitely many fractions equivalent to 1/4. This is because you can multiply the numerator (1) and the denominator (4) by any non-zero whole number. Let's explore a few examples:
Multiplying by Whole Numbers
- Multiplying by 2: (1 x 2) / (4 x 2) = 2/8
- Multiplying by 3: (1 x 3) / (4 x 3) = 3/12
- Multiplying by 4: (1 x 4) / (4 x 4) = 4/16
- Multiplying by 5: (1 x 5) / (4 x 5) = 5/20
- Multiplying by 10: (1 x 10) / (4 x 10) = 10/40
And so on. You can continue this process indefinitely, generating an infinite number of equivalent fractions.
Visualizing Equivalent Fractions
Visual aids can be incredibly helpful in grasping the concept of equivalent fractions. Imagine a rectangle divided into four equal parts. One of those parts represents 1/4. Now, imagine dividing that same rectangle into eight equal parts. Two of those smaller parts represent the same area as the original one-quarter, thus illustrating that 1/4 is equivalent to 2/8. You can extend this visualization to other equivalent fractions by further dividing the rectangle.
Simplifying Fractions and Finding 1/4
While we can create infinitely many equivalent fractions by multiplying, we can also simplify fractions by dividing both the numerator and denominator by their greatest common divisor (GCD). This process reduces the fraction to its simplest form.
Let's consider some fractions and determine if they are equivalent to 1/4:
- 2/8: The GCD of 2 and 8 is 2. Dividing both by 2 gives 1/4. Therefore, 2/8 is equivalent to 1/4.
- 3/12: The GCD of 3 and 12 is 3. Dividing both by 3 gives 1/4. Therefore, 3/12 is equivalent to 1/4.
- 5/20: The GCD of 5 and 20 is 5. Dividing both by 5 gives 1/4. Therefore, 5/20 is equivalent to 1/4.
- 100/400: The GCD of 100 and 400 is 100. Dividing both by 100 gives 1/4. Therefore, 100/400 is equivalent to 1/4.
By simplifying fractions, we can identify if they are equivalent to 1/4. This process is crucial in simplifying calculations and presenting answers in their most concise form.
Practical Applications of Equivalent Fractions
Understanding and working with equivalent fractions is not just an abstract mathematical concept; it has numerous practical applications in everyday life and various professions:
Cooking and Baking
Recipes often require fractional measurements. Knowing equivalent fractions allows for adjustments based on available ingredients or desired yield. For example, if a recipe calls for 1/4 cup of sugar, you can use 2/8 cup or 3/12 cup as an equivalent.
Construction and Engineering
Precise measurements are paramount in construction and engineering. Understanding equivalent fractions ensures accuracy in calculations involving dimensions, materials, and proportions.
Finance and Accounting
Equivalent fractions play a role in calculating percentages, proportions, and ratios, crucial aspects of financial management and accounting.
Data Analysis and Statistics
Data analysis often involves representing data as fractions and proportions. The ability to identify and work with equivalent fractions is essential for accurate interpretations and comparisons.
Identifying Equivalent Fractions: A Step-by-Step Guide
Here’s a structured approach to determine whether a given fraction is equivalent to 1/4:
-
Simplify the Fraction: Reduce the given fraction to its simplest form by dividing both the numerator and denominator by their greatest common divisor (GCD).
-
Compare to 1/4: Once simplified, compare the resulting fraction to 1/4. If they are identical, the original fraction is equivalent to 1/4.
-
Cross-Multiplication: An alternative method is to use cross-multiplication. Multiply the numerator of the first fraction by the denominator of the second fraction and vice-versa. If the products are equal, the fractions are equivalent. For example, to check if 2/8 is equivalent to 1/4: (2 x 4) = 8 and (8 x 1) = 8. Since the products are equal, the fractions are equivalent.
Common Mistakes to Avoid
When working with equivalent fractions, be mindful of these common errors:
-
Only multiplying or dividing the numerator or denominator: Remember, to maintain equivalence, you must perform the same operation (multiplication or division) on both the numerator and denominator.
-
Incorrectly finding the GCD: Ensure you correctly identify the greatest common divisor when simplifying fractions. An inaccurate GCD will lead to an incorrect simplified fraction.
-
Confusing equivalent fractions with addition/subtraction: Equivalent fractions represent the same value, not the result of adding or subtracting fractions.
Advanced Concepts and Extensions
The concept of equivalent fractions extends to more complex mathematical contexts:
-
Working with decimals: Equivalent fractions can be converted to decimals and vice-versa, allowing for flexible calculations involving fractions and decimals.
-
Algebraic expressions: Equivalent fractions are used extensively in algebraic manipulations and equation solving.
-
Ratio and proportion: Equivalent fractions are the backbone of understanding and solving problems related to ratios and proportions.
-
Geometry and measurement: Fractions and their equivalents are integral to geometric calculations involving areas, volumes, and angles.
Conclusion
Understanding equivalent fractions, particularly those equivalent to 1/4, is a cornerstone of mathematical literacy. From everyday tasks to complex scientific calculations, the ability to identify, simplify, and utilize equivalent fractions is essential. Mastering this concept lays a solid foundation for further mathematical explorations and enhances problem-solving skills across various fields. This guide provides a comprehensive framework to confidently navigate the world of equivalent fractions and apply them effectively in diverse scenarios. Continuous practice and application are key to solidifying your understanding and building confidence in working with fractions.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Fractions Are Equivalent To 1/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.