What Fractions Are Equivalent To 2/5
News Co
Mar 28, 2025 · 5 min read
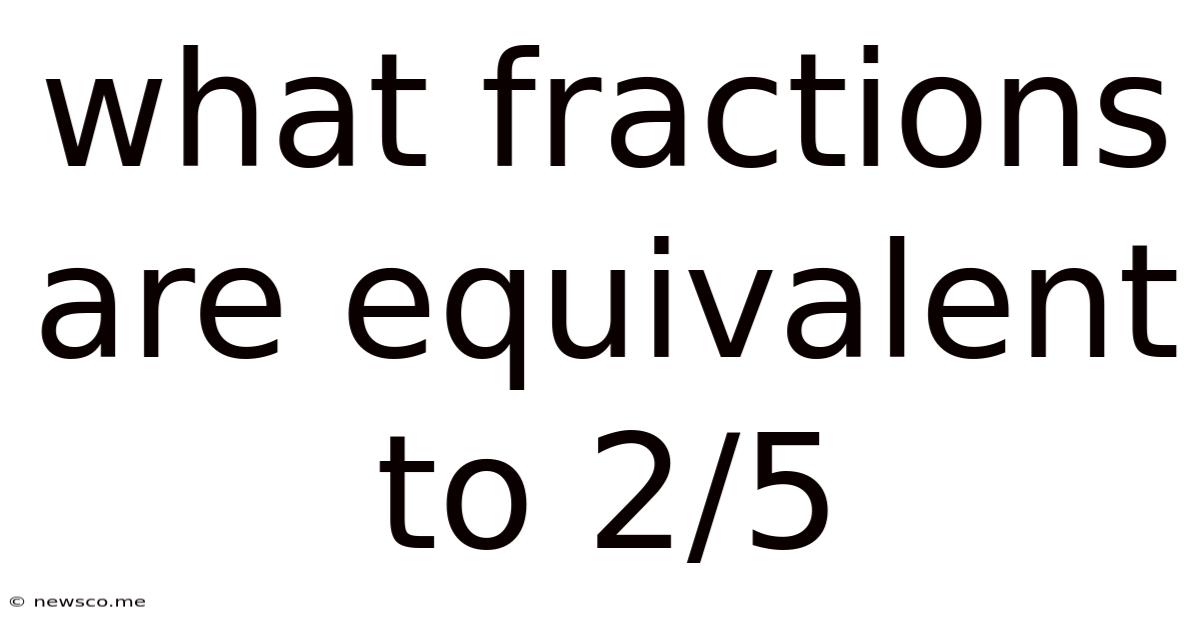
Table of Contents
What Fractions Are Equivalent to 2/5? A Comprehensive Guide
Understanding equivalent fractions is a fundamental concept in mathematics, crucial for simplifying calculations, comparing quantities, and grasping more advanced mathematical concepts. This comprehensive guide delves into the world of equivalent fractions, focusing specifically on fractions equivalent to 2/5. We'll explore various methods for finding these equivalents, delve into the underlying principles, and provide practical examples to solidify your understanding.
Understanding Equivalent Fractions
Equivalent fractions represent the same proportion or value, even though they look different. Think of it like slicing a pizza: one-half (1/2) is the same as two-quarters (2/4), or four-eighths (4/8), despite the differing number of slices. The key is that the ratio between the numerator (top number) and the denominator (bottom number) remains constant.
To find equivalent fractions, you simply multiply or divide both the numerator and the denominator by the same non-zero number. This process maintains the original ratio and thus creates an equivalent fraction. This is because multiplying or dividing both the numerator and denominator by the same number is the same as multiplying or dividing the fraction by 1 (since any number divided by itself equals 1).
Methods for Finding Equivalent Fractions of 2/5
Let's explore various techniques to generate fractions equivalent to 2/5:
1. Multiplication Method:
This is the most straightforward approach. Choose any whole number (except zero) and multiply both the numerator (2) and the denominator (5) by that number.
- Multiply by 2: (2 x 2) / (5 x 2) = 4/10
- Multiply by 3: (2 x 3) / (5 x 3) = 6/15
- Multiply by 4: (2 x 4) / (5 x 4) = 8/20
- Multiply by 5: (2 x 5) / (5 x 5) = 10/25
- Multiply by 10: (2 x 10) / (5 x 10) = 20/50
- Multiply by 100: (2 x 100) / (5 x 100) = 200/500
As you can see, this method generates an infinite number of equivalent fractions. You can continue multiplying by any whole number to create more.
2. Division Method (Simplification):
While the multiplication method creates larger equivalent fractions, division (also known as simplification or reducing to lowest terms) helps find smaller, equivalent fractions. This involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. The GCD is the largest number that divides both the numerator and denominator without leaving a remainder.
In the case of 2/5, the GCD of 2 and 5 is 1. Since dividing both by 1 doesn't change the fraction, 2/5 is already in its simplest form. This means there are no smaller equivalent fractions.
3. Visual Representation:
Visual aids can help understand equivalent fractions. Imagine a rectangle divided into five equal parts, with two parts shaded (representing 2/5). Now, imagine dividing each of those five parts in half. You now have ten parts, and four are shaded, representing 4/10, which is equivalent to 2/5. This visual approach reinforces the concept of maintaining the same proportion.
Illustrative Examples: Comparing Fractions Equivalent to 2/5
Let's use some examples to compare fractions equivalent to 2/5 and demonstrate their equality:
Example 1: Comparing 2/5 and 4/10
We can use cross-multiplication to verify their equivalence:
2 x 10 = 20 5 x 4 = 20
Since the products are equal, the fractions 2/5 and 4/10 are equivalent.
Example 2: Comparing 2/5 and 6/15
Again, using cross-multiplication:
2 x 15 = 30 5 x 6 = 30
The equal products confirm the equivalence of 2/5 and 6/15.
Example 3: Real-World Application
Imagine you have a recipe that calls for 2/5 of a cup of sugar. You could equally use 4/10 of a cup, 6/15 of a cup, or any other equivalent fraction. The amount of sugar will remain the same.
The Importance of Understanding Equivalent Fractions
Mastering equivalent fractions is essential for several reasons:
- Simplifying Fractions: Reducing fractions to their simplest form (lowest terms) makes them easier to work with and understand.
- Comparing Fractions: Equivalent fractions allow you to compare fractions with different denominators by finding a common denominator.
- Adding and Subtracting Fractions: You need to find equivalent fractions with a common denominator before adding or subtracting them.
- Solving Equations: Many algebraic equations involve fractions, and understanding equivalent fractions is crucial for manipulating and solving these equations.
- Real-world Applications: Numerous real-world situations involve fractions, from cooking and baking to construction and engineering.
Beyond the Basics: Exploring Decimal and Percentage Equivalents
Equivalent fractions can also be expressed as decimals and percentages. To find the decimal equivalent of 2/5, simply divide the numerator (2) by the denominator (5):
2 ÷ 5 = 0.4
To express this as a percentage, multiply the decimal by 100:
0.4 x 100 = 40%
Therefore, 2/5 is equivalent to 0.4 and 40%. All equivalent fractions of 2/5 will also have the same decimal and percentage equivalents. For instance, 4/10 also equals 0.4 or 40%.
Common Mistakes to Avoid
While finding equivalent fractions is relatively straightforward, here are some common mistakes to watch out for:
- Adding or subtracting the numerator and denominator: This is incorrect. You must multiply or divide both the numerator and the denominator by the same number.
- Using zero as a multiplier or divisor: You cannot multiply or divide by zero.
- Incorrectly identifying the greatest common divisor: This can lead to incomplete simplification.
Practice Makes Perfect
The best way to solidify your understanding of equivalent fractions is through practice. Try generating various equivalent fractions for 2/5 and compare them using cross-multiplication. Explore real-world applications and work through example problems to build your confidence and skill. Understanding equivalent fractions is a building block for more advanced mathematical concepts, so it's a skill worth mastering.
Conclusion
Finding fractions equivalent to 2/5, or any fraction for that matter, is a fundamental skill in mathematics. By understanding the principles of multiplication and division, and utilizing techniques like cross-multiplication, you can confidently generate and compare equivalent fractions. This knowledge extends far beyond the classroom, finding practical applications in everyday life and more advanced mathematical contexts. Consistent practice will solidify your understanding and make working with fractions much easier. Remember to always verify your work through methods like cross-multiplication to ensure accuracy and build a strong foundation in this crucial mathematical concept.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Fractions Are Equivalent To 2/5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.