What Is 1 1 3 Times 3
News Co
Mar 30, 2025 · 5 min read
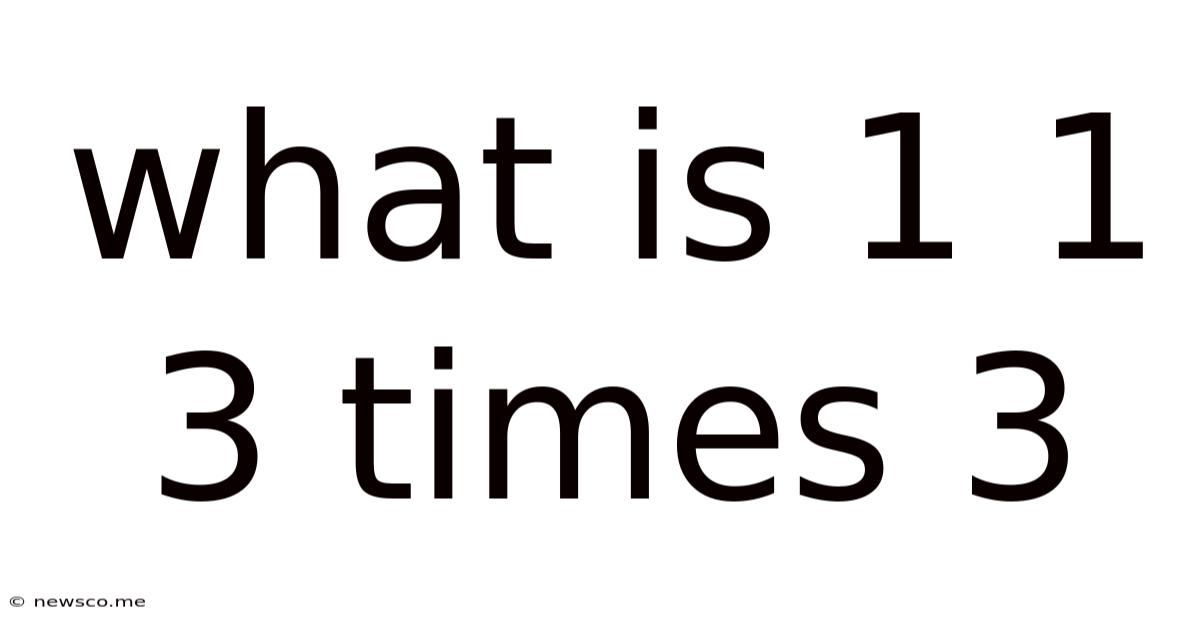
Table of Contents
What is 1 + 1 + 3 times 3? Understanding Order of Operations (PEMDAS/BODMAS)
The seemingly simple question, "What is 1 + 1 + 3 times 3?" often trips people up, highlighting the crucial importance of understanding the order of operations. This article will not only solve the equation but also delve into the underlying mathematical principles, exploring common mistakes and offering practical tips to avoid them. We'll also examine how this concept relates to more complex mathematical problems and programming.
The Importance of Order of Operations (PEMDAS/BODMAS)
The order of operations, often remembered by the acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction), dictates the sequence in which mathematical operations should be performed. Failing to follow this order can lead to incorrect results.
PEMDAS/BODMAS is crucial because:
- Consistency: It ensures that everyone arrives at the same answer for a given mathematical expression, regardless of their background or interpretation. Without a standardized order, mathematical communication would be chaotic.
- Accuracy: Following the order of operations guarantees accurate calculations, particularly in complex equations. Skipping steps or performing operations out of order can lead to significant errors.
- Foundation of Higher Mathematics: It forms the basis for more advanced mathematical concepts, including algebra, calculus, and beyond. Mastering the order of operations is essential for success in these fields.
Solving the Equation: 1 + 1 + 3 times 3
Now, let's tackle the equation: 1 + 1 + 3 times 3. According to PEMDAS/BODMAS:
-
Multiplication first: We perform the multiplication operation before addition. 3 times 3 equals 9. The equation now becomes: 1 + 1 + 9.
-
Addition: Finally, we add the numbers together: 1 + 1 + 9 = 11.
Therefore, the answer is 11.
Common Mistakes and Misinterpretations
A common mistake is to perform the addition operations from left to right without considering the order of operations. This would lead to an incorrect answer:
1 + 1 + 3 = 5; 5 x 3 = 15. This is wrong!
This illustrates the critical importance of prioritizing multiplication and division before addition and subtraction. Understanding and applying PEMDAS/BODMAS correctly is non-negotiable for accurate mathematical calculations.
PEMDAS/BODMAS in Different Contexts
The principles of PEMDAS/BODMAS extend beyond simple arithmetic. They are fundamental to:
-
Algebra: Solving algebraic equations often involves multiple operations, and following the order of operations is essential to isolate variables and find solutions.
-
Calculus: Derivatives and integrals often involve complex expressions requiring careful application of the order of operations.
-
Programming: Programming languages strictly adhere to the order of operations. Understanding this is vital for writing correct and efficient code. Different programming languages might use slightly different symbols, but the underlying principle remains the same. For instance, the
*symbol universally represents multiplication, while+represents addition. -
Data Science: In data analysis and scientific computing, PEMDAS/BODMAS is essential when dealing with formulas and calculations within datasets. Applying the order of operations ensures accurate results and reliable interpretations of data.
Advanced Applications and Extensions
The order of operations becomes increasingly important as we deal with more complex expressions. Consider examples with parentheses or exponents:
-
Parentheses/Brackets: Parentheses or brackets dictate that the operations within them must be performed first, regardless of the usual PEMDAS/BODMAS order. For example: (1 + 1) + 3 * 3 = 2 + 9 = 11, or 1 + (1 + 3) * 3 = 1 + 12 = 13.
-
Exponents/Orders: Exponents (or orders) represent repeated multiplication and must be calculated before other operations. For example: 1 + 1 + 3^2 (3 squared) = 1 + 1 + 9 = 11.
Practical Tips for Avoiding Mistakes
- Write Clearly: Write out your calculations step-by-step, clearly indicating the order of operations. This helps avoid confusion and errors.
- Use Parentheses: Use parentheses to group operations that should be performed together. This is especially important for clarity when dealing with complex expressions.
- Check Your Work: Always double-check your calculations. Using a calculator can be helpful, but it's crucial to understand the underlying principles.
- Practice: Regular practice is key to mastering the order of operations. Work through various problems of increasing complexity.
Beyond the Basics: Exploring Related Concepts
While the primary focus is on PEMDAS/BODMAS, understanding related mathematical concepts enhances comprehension. These include:
-
Associative Property: This property states that the grouping of numbers in addition or multiplication does not affect the result. For example: (1 + 1) + 3 = 1 + (1 + 3).
-
Commutative Property: This property states that the order of numbers in addition or multiplication does not affect the result. For example: 1 + 3 = 3 + 1.
-
Distributive Property: This property states that multiplying a number by a sum is equivalent to multiplying the number by each term in the sum and then adding the results. For example: 3 * (1 + 2) = (3 * 1) + (3 * 2).
Understanding these properties alongside PEMDAS/BODMAS provides a more comprehensive grasp of arithmetic and lays a strong foundation for advanced mathematical studies.
Conclusion: Mastering the Fundamentals
The simple equation, 1 + 1 + 3 times 3, serves as a powerful reminder of the importance of understanding the order of operations. By adhering to PEMDAS/BODMAS, we ensure accurate and consistent mathematical calculations. Mastering these principles is not just about solving simple equations; it’s about building a solid foundation for success in more complex mathematical endeavors, programming, and various scientific fields. Remember to practice regularly, use clear notation, and always double-check your work to avoid common pitfalls. The ability to correctly interpret and solve mathematical expressions is a fundamental skill applicable across numerous disciplines. Consistent application of PEMDAS/BODMAS and an understanding of related mathematical properties contribute to accurate calculations and a deeper appreciation of mathematics as a whole.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 1 1 3 Times 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.