What Is 1 2/3 As A Decimal
News Co
Apr 05, 2025 · 5 min read
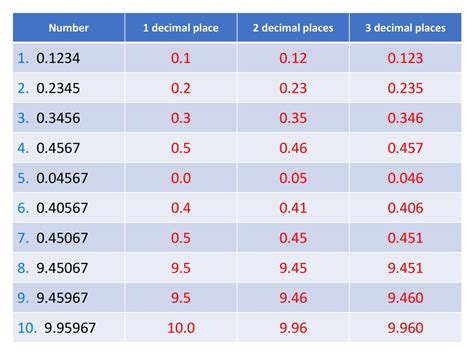
Table of Contents
What is 1 2/3 as a Decimal? A Comprehensive Guide
Converting fractions to decimals is a fundamental skill in mathematics with applications spanning various fields. This comprehensive guide will walk you through the process of converting the mixed number 1 2/3 into its decimal equivalent, explaining the underlying concepts and providing practical examples to solidify your understanding. We'll explore multiple methods, catering to different learning styles and mathematical preferences.
Understanding Mixed Numbers and Fractions
Before diving into the conversion, let's clarify the terminology. A mixed number combines a whole number and a fraction, like 1 2/3. Here, '1' represents the whole number, and '2/3' is the fraction, indicating two parts out of three equal parts. A fraction, in essence, represents a part of a whole. The top number (2) is the numerator, representing the number of parts you have, and the bottom number (3) is the denominator, representing the total number of equal parts the whole is divided into.
Method 1: Converting the Fraction to a Decimal then Adding the Whole Number
This is arguably the most straightforward approach. We'll first convert the fractional part (2/3) into a decimal and then add the whole number (1).
Step 1: Divide the Numerator by the Denominator
To convert the fraction 2/3 to a decimal, we perform the division: 2 ÷ 3.
This division results in a repeating decimal: 0.666666... This is often represented as 0.6̅, where the bar indicates the repeating digit.
Step 2: Add the Whole Number
Now, add the whole number (1) to the decimal equivalent of the fraction (0.666666...):
1 + 0.666666... = 1.666666...
Therefore, 1 2/3 as a decimal is approximately 1.667 (rounding to three decimal places). It's crucial to understand that this is an approximation because the decimal representation of 2/3 is a non-terminating, repeating decimal.
Method 2: Converting the Mixed Number to an Improper Fraction
This method involves transforming the mixed number into an improper fraction first, and then converting the improper fraction to a decimal. An improper fraction has a numerator larger than or equal to its denominator.
Step 1: Convert to an Improper Fraction
To convert 1 2/3 to an improper fraction, we multiply the whole number (1) by the denominator (3), add the numerator (2), and keep the same denominator (3):
(1 × 3) + 2 = 5
The improper fraction becomes 5/3.
Step 2: Divide the Numerator by the Denominator
Now, divide the numerator (5) by the denominator (3):
5 ÷ 3 = 1.666666...
This again gives us the repeating decimal 1.666666..., which is approximately 1.667 when rounded to three decimal places.
Method 3: Using a Calculator
Modern calculators readily handle fraction-to-decimal conversions. Simply enter the mixed number, either as 1 2/3 (if your calculator supports this format) or as 5/3 (after converting to an improper fraction), and press the equals (=) button. The calculator will directly provide the decimal equivalent, which will likely be displayed as 1.666666... or a rounded version like 1.667.
Understanding Repeating Decimals
The decimal representation of 1 2/3 highlights the concept of repeating decimals. These are decimals with a sequence of digits that repeats infinitely. In this case, the digit '6' repeats indefinitely. While calculators often round these decimals, it's important to remember their true nature as non-terminating decimals. This distinction is crucial in various mathematical operations and applications.
Practical Applications: Where Decimal Conversions are Useful
Understanding fraction-to-decimal conversions is essential in many real-world scenarios:
- Measurement and Engineering: Converting fractions of inches or centimeters to decimals is commonplace in engineering, construction, and design.
- Finance and Accounting: Calculating percentages, interest rates, and proportions often involves working with both fractions and decimals.
- Data Analysis and Statistics: Representing data in decimal form is often necessary for calculations and visualizations.
- Programming and Computer Science: Many programming languages require numerical input in decimal format.
- Everyday Life: Dividing food, measuring ingredients, or sharing resources frequently requires fraction-to-decimal conversions for accurate distribution.
Beyond 1 2/3: Generalizing the Conversion Process
The methods outlined above can be applied to convert any mixed number or fraction into its decimal equivalent. The key steps remain the same:
- For mixed numbers: Convert the fractional part to a decimal through division, and then add the whole number.
- For fractions: Divide the numerator by the denominator to obtain the decimal representation.
- Dealing with repeating decimals: Recognize that some fractions will yield repeating decimals, and understand how to represent these using the bar notation (e.g., 0.6̅) or by rounding to a specified number of decimal places for practical applications.
Common Mistakes to Avoid
- Incorrect Order of Operations: When dealing with mixed numbers, ensure you add the whole number after converting the fraction to a decimal.
- Rounding Errors: Be mindful of rounding errors, especially when working with repeating decimals. Specify the level of precision required (e.g., rounding to three decimal places).
- Misinterpreting the Fraction: Double-check that you are correctly identifying the numerator and the denominator before performing the division.
Conclusion: Mastering Decimal Conversions
Converting fractions like 1 2/3 to decimals is a fundamental skill that enhances mathematical proficiency. This guide has equipped you with multiple methods and a comprehensive understanding of the underlying concepts. By understanding repeating decimals, practical applications, and potential pitfalls, you're well-prepared to confidently tackle various fraction-to-decimal conversions in your studies and daily life. Remember that while calculators offer convenience, a strong conceptual understanding ensures accurate and efficient results.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 1 2/3 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.