What Is 1 2/3 Plus 1 2/3
News Co
May 07, 2025 · 5 min read
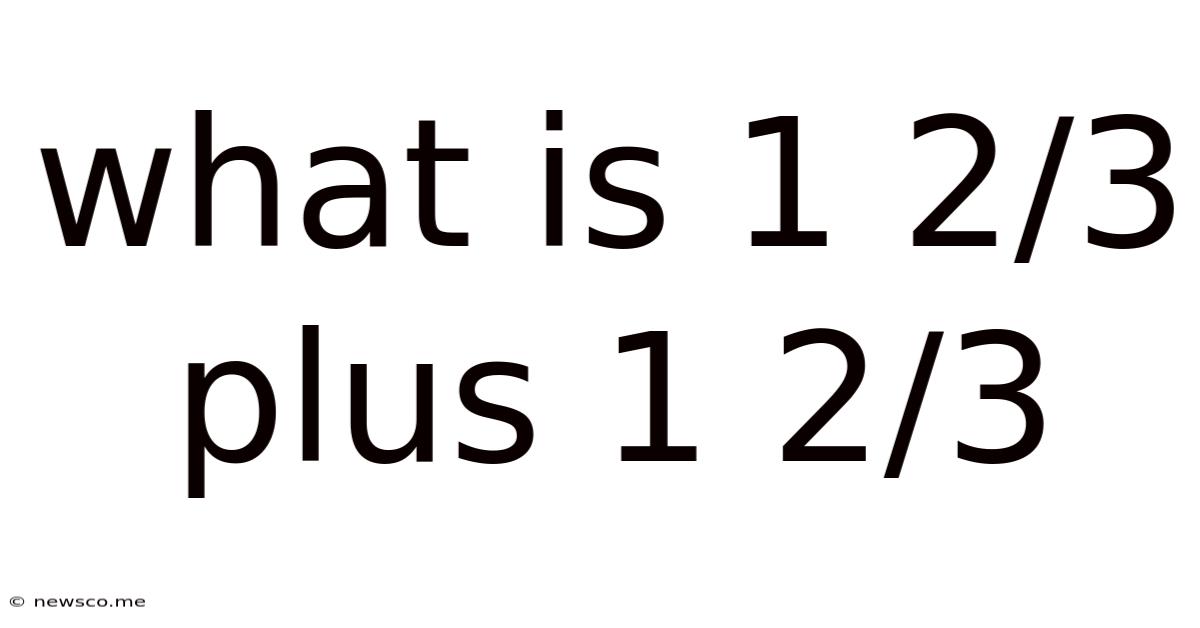
Table of Contents
What is 1 2/3 Plus 1 2/3? A Deep Dive into Fraction Addition
Adding fractions might seem like a simple task, especially when dealing with mixed numbers like 1 2/3. However, understanding the underlying principles behind fraction addition is crucial for building a strong foundation in mathematics. This comprehensive guide will not only answer the question "What is 1 2/3 plus 1 2/3?" but also delve into the intricacies of fraction addition, providing you with the tools to tackle more complex problems with confidence.
Understanding Fractions: A Refresher
Before we jump into the addition, let's revisit the fundamental concepts of fractions. A fraction represents a part of a whole. It consists of two main components:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 2/3, the numerator is 2 (we have two parts), and the denominator is 3 (the whole is divided into three equal parts).
Mixed Numbers: Whole and Fractional Parts
A mixed number combines a whole number and a fraction. For instance, 1 2/3 means one whole unit plus two-thirds of another unit. Understanding this representation is key to adding mixed numbers effectively.
Adding Fractions with the Same Denominator
The simplest form of fraction addition involves fractions with the same denominator. In such cases, we simply add the numerators and keep the denominator unchanged. Let's illustrate with an example:
1/4 + 2/4 = (1 + 2)/4 = 3/4
Adding Mixed Numbers: A Step-by-Step Approach
Adding mixed numbers like 1 2/3 + 1 2/3 requires a slightly more structured approach. Here's a breakdown of the process:
Step 1: Add the Whole Numbers
First, add the whole number parts of the mixed numbers: 1 + 1 = 2
Step 2: Add the Fractions
Next, add the fractional parts: 2/3 + 2/3 = (2 + 2)/3 = 4/3
Step 3: Simplify the Result
The result from Step 2 (4/3) is an improper fraction (where the numerator is greater than the denominator). To simplify, we convert it to a mixed number:
4/3 = 1 1/3
Step 4: Combine Whole and Fractional Parts
Finally, combine the whole number sum from Step 1 and the simplified mixed number from Step 3:
2 + 1 1/3 = 3 1/3
Therefore, 1 2/3 + 1 2/3 = 3 1/3
Alternative Methods for Adding Mixed Numbers
While the step-by-step approach is straightforward, there are alternative methods that can be equally effective:
Method 1: Converting to Improper Fractions
Convert both mixed numbers into improper fractions before adding. An improper fraction has a numerator larger than or equal to the denominator.
- 1 2/3 = (1 x 3 + 2)/3 = 5/3
- 5/3 + 5/3 = 10/3
Then, convert the result back to a mixed number:
10/3 = 3 1/3
Method 2: Visual Representation
Visual aids, such as diagrams or number lines, can be particularly helpful for visualizing fraction addition. Drawing diagrams representing 1 2/3 and then combining them visually can help solidify the understanding of the addition process.
Expanding on Fraction Addition: Adding Fractions with Different Denominators
The examples above focused on fractions with the same denominator. However, adding fractions with different denominators requires finding a common denominator – a number that is a multiple of both denominators. This involves finding the least common multiple (LCM) of the denominators.
For example, let's add 1/2 and 1/3:
- Find the LCM of 2 and 3, which is 6.
- Convert both fractions to have a denominator of 6:
- 1/2 = 3/6
- 1/3 = 2/6
- Add the fractions: 3/6 + 2/6 = 5/6
Practical Applications of Fraction Addition
Understanding fraction addition is not just an academic exercise; it has numerous practical applications in daily life and various fields:
- Cooking and Baking: Following recipes often requires precise measurements, involving fractions.
- Construction and Engineering: Accurate calculations using fractions are essential in various aspects of construction and engineering projects.
- Finance: Dealing with percentages and proportions, fundamental concepts in finance, rely on the understanding of fractions.
- Data Analysis: In statistical analysis, understanding fractions is important for calculating proportions and percentages.
Troubleshooting Common Mistakes in Fraction Addition
Several common mistakes can occur when adding fractions:
- Forgetting to find a common denominator: This is a frequent error when adding fractions with different denominators.
- Incorrectly adding numerators and denominators: Remember, only the numerators are added; the denominator remains the same (when the denominators are the same).
- Not simplifying the result: Always simplify the final answer to its lowest terms.
Conclusion: Mastering Fraction Addition
Adding fractions, especially mixed numbers, is a fundamental mathematical skill. By understanding the principles of fractions, mixed numbers, and the process of finding common denominators, you can confidently tackle a wide range of fraction addition problems. This guide has provided multiple approaches to solving these problems, empowering you to choose the method most suitable for your understanding and problem-solving style. Remember to practice regularly to solidify your understanding and improve your proficiency in this important area of mathematics. The seemingly simple question "What is 1 2/3 plus 1 2/3?" opens a door to a wider understanding of the world of fractions and their practical applications. Mastering this skill provides a solid foundation for more advanced mathematical concepts.
Latest Posts
Latest Posts
-
How To Find The Ratio Of X To Y
May 08, 2025
-
15 Is 40 Of What Number
May 08, 2025
-
How Do You Write 0 00015 In Scientific Notation
May 08, 2025
-
The Number From Which Another Number Is Being Subtracted
May 08, 2025
-
How To Write 1 500 On A Check
May 08, 2025
Related Post
Thank you for visiting our website which covers about What Is 1 2/3 Plus 1 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.