What Is 1 2 Of 1 1 4
News Co
Mar 25, 2025 · 4 min read
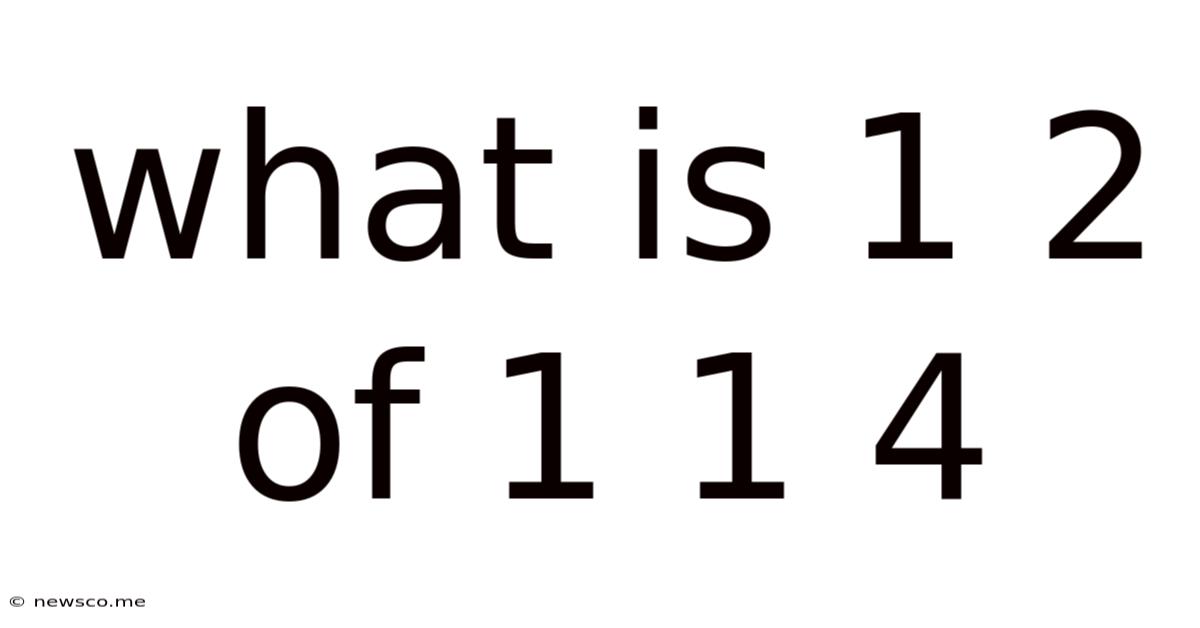
Table of Contents
What is 1/2 of 1 1/4? A Comprehensive Guide to Fraction Multiplication
Understanding fractions can sometimes feel like navigating a maze, but mastering them is crucial for various aspects of life, from baking to advanced mathematics. This article will delve deep into the seemingly simple question: "What is 1/2 of 1 1/4?" We'll not only provide the answer but also explore the underlying principles, different methods for solving the problem, and expand on related concepts to build a robust understanding of fraction manipulation.
Understanding the Question
The question "What is 1/2 of 1 1/4?" is essentially asking us to calculate the product of two fractions: 1/2 and 1 1/4. The word "of" in this context signifies multiplication. Therefore, the mathematical expression we need to solve is:
(1/2) * (1 1/4)
Before we proceed with the calculation, let's refresh our understanding of fractions and mixed numbers.
Fractions: A Quick Refresher
A fraction represents a part of a whole. It consists of two parts:
- Numerator: The top number, representing the number of parts we have.
- Denominator: The bottom number, representing the total number of equal parts the whole is divided into.
For example, in the fraction 3/4, the numerator is 3 and the denominator is 4. This means we have 3 parts out of a total of 4 equal parts.
Mixed Numbers: Deconstructing the Whole and the Part
A mixed number combines a whole number and a fraction. For instance, 1 1/4 represents one whole unit and an additional 1/4 of a unit. To perform calculations, it's often easier to convert mixed numbers into improper fractions.
Converting Mixed Numbers to Improper Fractions
To convert a mixed number to an improper fraction, follow these steps:
- Multiply the whole number by the denominator: In our example, 1 (whole number) * 4 (denominator) = 4.
- Add the result to the numerator: 4 + 1 (numerator) = 5.
- Keep the same denominator: The denominator remains 4.
Therefore, 1 1/4 is equivalent to the improper fraction 5/4.
Calculating 1/2 of 1 1/4: Two Methods
Now that we've converted our mixed number to an improper fraction, we can proceed with the multiplication. Let's explore two common methods:
Method 1: Direct Multiplication
This method involves multiplying the numerators together and the denominators together:
(1/2) * (5/4) = (1 * 5) / (2 * 4) = 5/8
Therefore, 1/2 of 1 1/4 is 5/8.
Method 2: Simplifying Before Multiplication
This method involves simplifying the fractions before multiplying. While not always necessary, it can make the calculation easier, especially with larger numbers. In this case, we can simplify by canceling out common factors:
(1/2) * (5/4) Notice that there are no common factors between the numerators and denominators in this example, so direct multiplication is the simplest approach.
Understanding the Result: 5/8
We've determined that 1/2 of 1 1/4 is 5/8. This means that if we divide 1 1/4 into two equal parts, each part will be 5/8. To visualize this, imagine a pizza cut into four slices. 1 1/4 pizzas would be 5 slices. Half of those 5 slices would be 2.5 slices, or 5/8 of a whole pizza.
Expanding on Fraction Operations
Understanding fraction multiplication is just one building block in the world of fractions. Let's briefly explore other essential operations:
Addition and Subtraction of Fractions
To add or subtract fractions, they must have a common denominator. If they don't, you need to find the least common multiple (LCM) of the denominators and convert the fractions accordingly. For example:
1/2 + 1/4 = 2/4 + 1/4 = 3/4
Division of Fractions
Dividing fractions involves inverting the second fraction (reciprocal) and then multiplying:
1/2 ÷ 1/4 = 1/2 * 4/1 = 4/2 = 2
Practical Applications of Fractions
Fractions are not just abstract mathematical concepts; they have numerous real-world applications:
- Cooking and Baking: Recipes often involve fractions of ingredients.
- Construction and Engineering: Precise measurements are crucial, and fractions play a vital role.
- Finance: Understanding fractions is important for managing budgets, calculating interest rates, and analyzing investments.
- Data Analysis: Fractions and percentages are essential for interpreting data and drawing conclusions.
Mastering Fractions: Tips and Resources
Mastering fractions takes practice. Here are some tips to improve your understanding:
- Regular Practice: Solve various fraction problems regularly to build confidence and fluency.
- Visual Aids: Use diagrams, charts, or real-world objects to visualize fractions.
- Online Resources: Many websites and educational platforms offer interactive lessons and practice exercises on fractions.
- Seek Help When Needed: Don't hesitate to ask teachers, tutors, or peers for help if you're struggling with a particular concept.
Conclusion
This comprehensive guide has explored the calculation of "What is 1/2 of 1 1/4?", demonstrating two methods to arrive at the solution of 5/8. Beyond the specific calculation, we've emphasized the broader understanding of fractions, their operations, and their relevance in various aspects of life. By mastering fractions, you equip yourself with a fundamental tool for tackling numerous mathematical challenges and real-world problems. Remember that consistent practice and a willingness to explore different methods are key to mastering this crucial mathematical concept. Continue to explore and delve deeper into the fascinating world of fractions—the possibilities are endless!
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 1 2 Of 1 1 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.