What Is 1/2 Of 1/5 In Fraction
News Co
Apr 28, 2025 · 5 min read
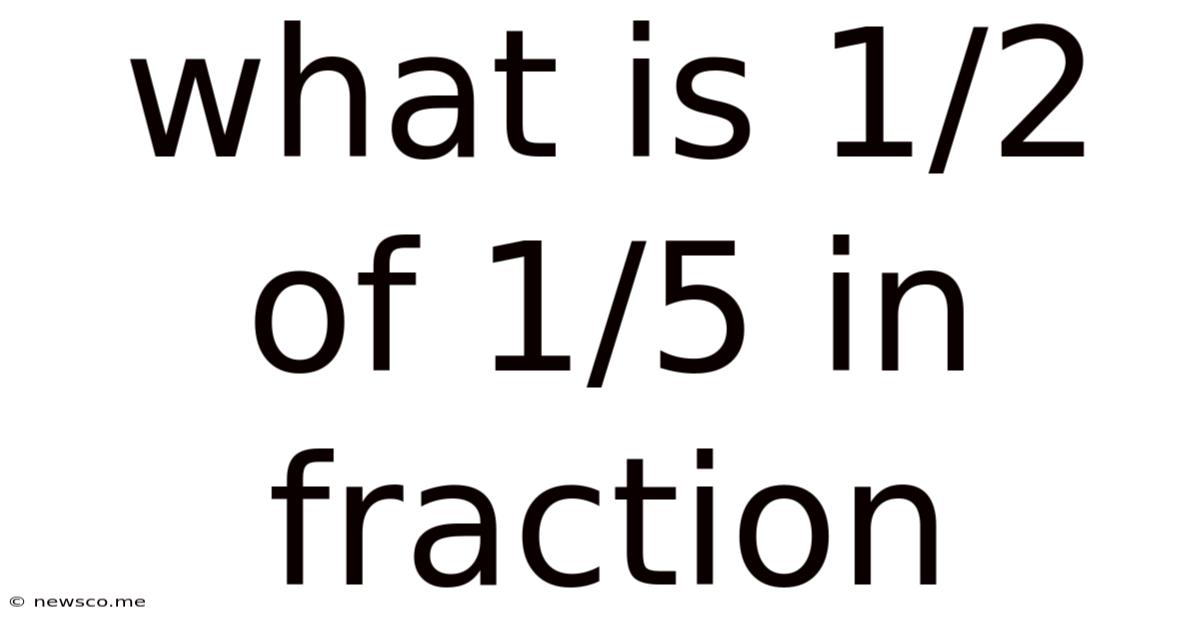
Table of Contents
What is 1/2 of 1/5 in Fraction? A Comprehensive Guide to Fraction Multiplication
Understanding fractions is a fundamental aspect of mathematics, crucial for various applications in everyday life and advanced studies. This comprehensive guide will delve into the process of finding half of a fifth, explaining the concepts involved and providing practical examples to solidify your understanding. We'll explore the mechanics of fraction multiplication, address common misconceptions, and offer tips for mastering fraction calculations.
Understanding Fractions: A Quick Recap
Before we dive into the calculation of 1/2 of 1/5, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two essential components:
- Numerator: The top number, indicating the number of parts we're considering.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For instance, in the fraction 1/5, the numerator (1) signifies one part, and the denominator (5) signifies that the whole is divided into five equal parts.
Multiplying Fractions: The Core Concept
Multiplying fractions involves a straightforward process: multiply the numerators together to obtain the new numerator, and multiply the denominators together to obtain the new denominator. This can be represented mathematically as:
(a/b) * (c/d) = (a * c) / (b * d)
Where 'a', 'b', 'c', and 'd' represent numerical values.
Calculating 1/2 of 1/5
Now, let's apply this knowledge to find 1/2 of 1/5. This can be expressed as a multiplication problem:
(1/2) * (1/5)
Following the rule for multiplying fractions:
- Multiply the numerators: 1 * 1 = 1
- Multiply the denominators: 2 * 5 = 10
Therefore, the result is:
1/10
This means that half of one-fifth is one-tenth.
Visualizing the Calculation
Visual aids can significantly enhance understanding. Imagine a rectangle representing a whole. Divide this rectangle into five equal parts. Shading one of these parts represents 1/5. Now, divide each of the five parts in half. Shading one of these smaller halves represents 1/10, which is half of 1/5.
Real-World Applications: Understanding the Significance
Understanding fraction multiplication extends far beyond abstract mathematical exercises. It finds practical application in various real-world scenarios:
-
Cooking and Baking: Scaling recipes up or down often involves fraction multiplication. For instance, if a recipe calls for 1/2 cup of flour and you want to make half the recipe, you would calculate 1/2 of 1/2, which is 1/4 cup of flour.
-
Construction and Engineering: Precise measurements are critical in these fields. Fraction multiplication helps in calculating material requirements and dimensions. For example, determining the length of a beam requiring 1/3 of a 1/2-meter plank.
-
Finance: Calculating percentages, interest, and shares often involves fraction multiplication. For example, determining the commission earned on a sale worth a fraction of the total sales volume.
-
Data Analysis and Statistics: Fractions are extensively used in data representation and analysis. Understanding fraction multiplication is crucial for interpreting data and making informed decisions.
Addressing Common Mistakes and Misconceptions
While fraction multiplication is relatively straightforward, several common errors can arise:
-
Incorrect Numerator and Denominator Multiplication: A frequent error is reversing the numerators and denominators during multiplication. Carefully pay attention to which number is the numerator and which is the denominator.
-
Forgetting to Simplify: After calculating the product, remember to simplify the resulting fraction to its lowest terms. This involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by the GCD. For instance, 2/4 simplifies to 1/2.
-
Incorrect Interpretation of "Of": The word "of" in fraction problems usually signifies multiplication. Understanding this is key to setting up the problem correctly.
-
Difficulty with Mixed Numbers: When dealing with mixed numbers (a whole number and a fraction, like 1 1/2), convert them into improper fractions (where the numerator is larger than the denominator) before multiplying. For example, 1 1/2 becomes 3/2.
Mastering Fraction Multiplication: Tips and Practice
Mastering fraction multiplication requires consistent practice and a solid grasp of the underlying principles. Here are some tips:
-
Start with Simple Fractions: Begin with straightforward examples to build a solid foundation. Gradually increase the complexity as your confidence grows.
-
Use Visual Aids: Visual representations, like diagrams and models, can greatly enhance understanding.
-
Practice Regularly: Consistent practice is key to mastering any mathematical concept. Solve numerous problems to reinforce your understanding.
-
Seek Help When Needed: Don't hesitate to seek clarification from teachers, tutors, or online resources if you encounter difficulties.
Expanding on Fraction Operations: Beyond Multiplication
While this article focuses on multiplication, a comprehensive understanding of fractions includes proficiency in addition, subtraction, and division as well.
-
Addition and Subtraction: Adding or subtracting fractions requires a common denominator. If the denominators are different, find the least common multiple (LCM) and convert the fractions to equivalent fractions with the LCM as the denominator. Then, add or subtract the numerators.
-
Division: Dividing fractions involves inverting the second fraction (the divisor) and multiplying. For example, (a/b) ÷ (c/d) = (a/b) * (d/c).
Mastering these four operations (addition, subtraction, multiplication, and division) provides a strong foundation for more advanced mathematical concepts.
Conclusion: The Power of Understanding Fractions
Understanding fraction multiplication, particularly solving problems like "What is 1/2 of 1/5?", is a crucial skill applicable to numerous facets of life. By mastering the principles outlined in this guide, and by dedicating time to consistent practice, you'll develop a strong foundation in fractions, enhancing your mathematical abilities and opening doors to a deeper understanding of the world around you. Remember to break down complex problems into smaller, manageable steps, and always double-check your work to minimize errors. With practice and patience, you can confidently tackle any fraction-related challenge. This strong foundation will serve you well in future mathematical endeavors.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 1/2 Of 1/5 In Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.