What Is 1 2 Of 5
News Co
Apr 06, 2025 · 5 min read
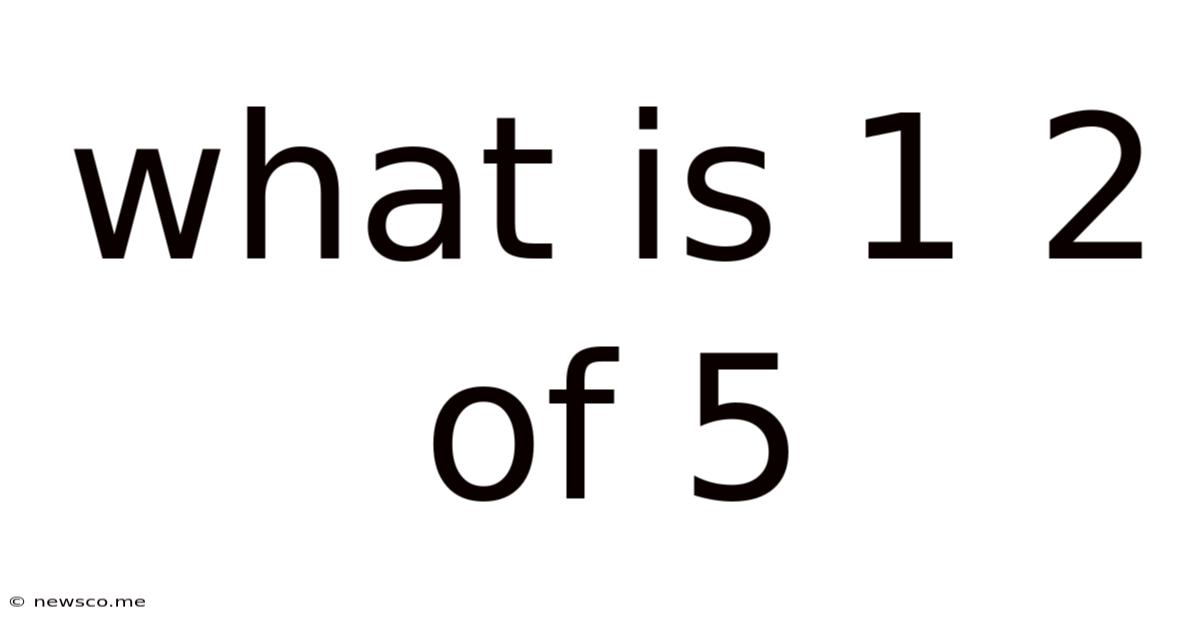
Table of Contents
What is 1/2 of 5? A Comprehensive Guide to Fractions and Their Applications
Understanding fractions is a fundamental aspect of mathematics, crucial for various applications in everyday life and advanced studies. This comprehensive guide will delve into the question, "What is 1/2 of 5?", exploring the concept of fractions, different methods of calculation, and practical examples demonstrating their relevance. We'll go beyond a simple answer and unpack the underlying principles, equipping you with the knowledge to confidently tackle similar fractional problems.
Understanding Fractions: A Quick Refresher
A fraction represents a part of a whole. It's composed of two main parts:
- Numerator: The top number indicates how many parts we have.
- Denominator: The bottom number shows the total number of equal parts the whole is divided into.
In our case, 1/2 represents one out of two equal parts. The numerator is 1, and the denominator is 2. Understanding this basic structure is key to solving fractional problems.
Calculating 1/2 of 5: Three Approaches
There are several ways to calculate half of 5. Let's explore three common methods:
Method 1: Direct Multiplication
The most straightforward method involves multiplying the fraction (1/2) by the whole number (5). Remember that any whole number can be expressed as a fraction with a denominator of 1 (e.g., 5 = 5/1).
Therefore, the calculation becomes:
(1/2) * (5/1) = (1 * 5) / (2 * 1) = 5/2
This results in an improper fraction (where the numerator is larger than the denominator). To convert it to a mixed number (a whole number and a fraction), we divide the numerator (5) by the denominator (2):
5 ÷ 2 = 2 with a remainder of 1
So, 5/2 is equivalent to 2 1/2.
Method 2: Division
Another approach is to divide the whole number (5) by the denominator of the fraction (2):
5 ÷ 2 = 2.5
This directly provides the decimal equivalent of the fraction. We can convert this decimal back to a mixed number:
2.5 = 2 and 0.5 (which is 1/2)
Therefore, the answer is again 2 1/2.
Method 3: Visual Representation
For a more intuitive understanding, we can visualize the problem. Imagine a pizza cut into 5 equal slices. To find half of the pizza, we divide the 5 slices into two equal groups. Each group will have 2 and a half slices. This visually confirms our answer of 2 1/2.
Expanding the Concept: Fractions and Their Real-World Applications
The ability to work with fractions isn't just an academic exercise; it's a practical skill applied in various everyday scenarios:
-
Cooking and Baking: Recipes frequently use fractions (e.g., 1/2 cup of sugar, 1/4 teaspoon of salt). Understanding fractions ensures accurate measurements and successful culinary outcomes.
-
Shopping and Budgeting: Discounts and sales are often expressed as fractions (e.g., 1/3 off, 25% which is 1/4 off). Calculating savings and managing budgets effectively requires fractional arithmetic.
-
Measurement and Construction: In construction and engineering, precise measurements are vital, often involving fractional units (e.g., inches, feet). Accurate calculations using fractions are crucial for projects to succeed.
-
Time Management: Dividing your time effectively involves understanding fractions. For instance, dedicating 1/3 of your day to work, 1/4 to personal activities, and the remaining fraction to other pursuits.
-
Data Analysis and Statistics: Fractions and percentages (which are simply fractions with a denominator of 100) are fundamental to data analysis, probability, and statistics. Understanding data requires the ability to interpret and work with fractions.
Beyond 1/2 of 5: Tackling More Complex Fractional Problems
The principles applied to calculating 1/2 of 5 can be extended to solve more complex problems involving different fractions and whole numbers. Let's consider some examples:
Example 1: Finding 2/3 of 9
- Multiply the fractions: (2/3) * (9/1) = (2 * 9) / (3 * 1) = 18/3
- Simplify the fraction: 18 ÷ 3 = 6
Therefore, 2/3 of 9 is 6.
Example 2: Finding 3/4 of 12
- Multiply the fractions: (3/4) * (12/1) = (3 * 12) / (4 * 1) = 36/4
- Simplify the fraction: 36 ÷ 4 = 9
Therefore, 3/4 of 12 is 9.
Example 3: Finding 5/8 of 24
- Multiply the fractions: (5/8) * (24/1) = (5 * 24) / (8 * 1) = 120/8
- Simplify the fraction: 120 ÷ 8 = 15
Therefore, 5/8 of 24 is 15.
These examples illustrate the consistent application of the multiplication method. Remember to always simplify your answer to its lowest terms for a cleaner and more accurate result.
Mastering Fractions: Tips and Resources
To enhance your understanding and skills in working with fractions, consider these suggestions:
-
Practice Regularly: Consistent practice is crucial for mastering any mathematical concept. Solve various problems involving different fractions and whole numbers.
-
Use Visual Aids: Diagrams and visual representations can significantly improve your understanding, particularly when dealing with more complex fractions.
-
Online Resources: Numerous online resources, including interactive tutorials and practice exercises, are available to help you learn and reinforce your understanding of fractions.
-
Seek Help When Needed: Don't hesitate to ask for help from teachers, tutors, or peers if you encounter difficulties. Clear up any confusion promptly to avoid building misconceptions.
Conclusion: The Power of Fractional Understanding
Understanding fractions is essential for navigating various aspects of life, from everyday tasks to more complex academic and professional pursuits. While the question "What is 1/2 of 5?" might seem simple at first glance, it opens the door to understanding a broader concept that has far-reaching implications. By grasping the fundamental principles and applying the methods outlined in this guide, you'll be well-equipped to confidently handle fractional problems and unlock their practical applications in your daily life. Remember that consistent practice and seeking assistance when needed are crucial for mastering this fundamental mathematical skill. The power of understanding fractions lies in its versatility and widespread relevance.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 1 2 Of 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.