What Is 1/2 To The Power Of 2
News Co
Apr 16, 2025 · 5 min read
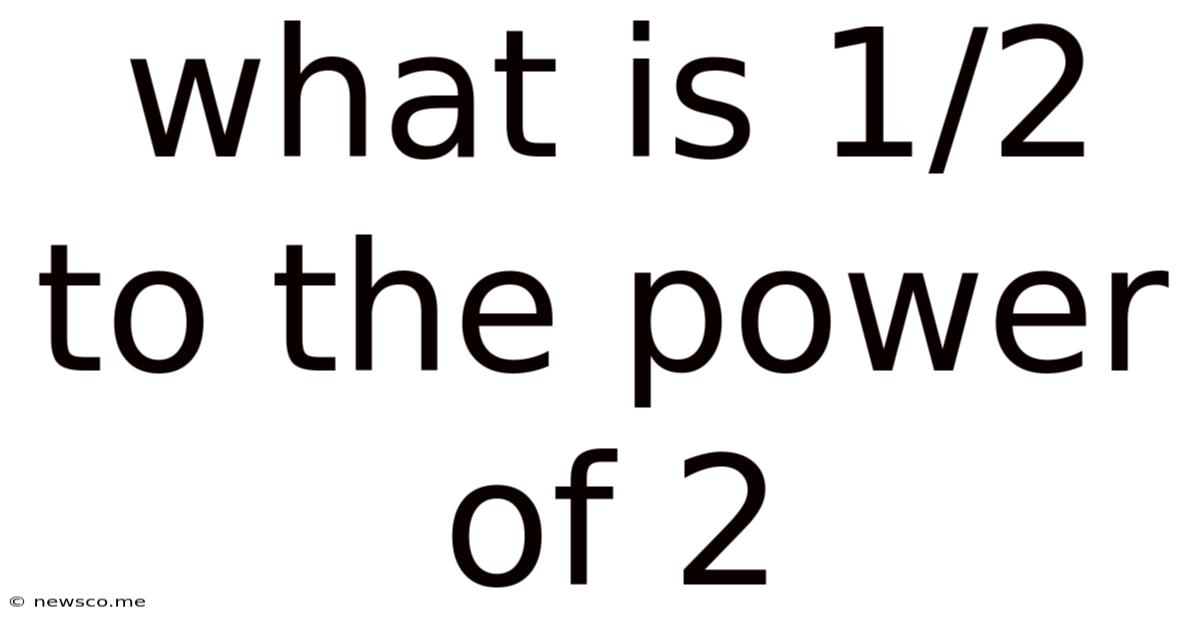
Table of Contents
What is 1/2 to the Power of 2? A Deep Dive into Fractional Exponents
The seemingly simple question, "What is 1/2 to the power of 2?" opens the door to a fascinating exploration of exponents, fractions, and their interplay in mathematics. While the answer itself is straightforward, understanding the underlying concepts solidifies a fundamental understanding of mathematical operations and lays the groundwork for tackling more complex problems. This comprehensive guide will not only provide the solution but also delve into the broader mathematical principles involved, ensuring a thorough grasp of the subject matter.
Understanding Exponents
Before tackling the specific problem, let's establish a firm understanding of exponents. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. For example:
- 2³ = 2 × 2 × 2 = 8 (2 raised to the power of 3, or 2 cubed)
- 5² = 5 × 5 = 25 (5 raised to the power of 2, or 5 squared)
- 10¹ = 10 (10 raised to the power of 1, simply equals itself)
- x⁰ = 1 (Any non-zero number raised to the power of 0 equals 1)
The exponent dictates the number of times the base is used as a factor in the multiplication. This seemingly simple concept extends to fractions and negative numbers, adding layers of complexity and nuance.
Fractional Exponents: A Bridge to Roots
The introduction of fractional exponents significantly expands the scope of exponential operations. A fractional exponent combines exponentiation and root extraction. Consider the general form:
x^(m/n)
This expression means: find the nth root of x and then raise the result to the power of m. Alternatively, you can raise x to the power of m and then take the nth root. Both approaches yield the same result.
For instance:
8^(2/3)
This can be calculated in two ways:
- (³√8)² = 2² = 4 (First, find the cube root of 8, which is 2. Then, square the result to get 4.)
- ³√(8²) = ³√64 = 4 (First, square 8 to get 64. Then, find the cube root of 64, which is also 4.)
This demonstrates the interchangeability of the processes – the order doesn't affect the final outcome. This principle is crucial in understanding the solution to our primary problem.
Solving 1/2 to the Power of 2
Now, let's apply this knowledge to the specific problem: (1/2)².
This expression means we are squaring the fraction 1/2. Remember, squaring a number means multiplying it by itself:
(1/2)² = (1/2) × (1/2)
To multiply fractions, we multiply the numerators together and the denominators together:
(1 × 1) / (2 × 2) = 1/4
Therefore, (1/2)² = 1/4
This simple calculation demonstrates the application of exponential rules to fractions. The exponent (2) indicates the number of times the fraction (1/2) is used as a factor in the multiplication.
Extending the Concept: Higher Powers and Negative Exponents
Let's explore what happens when we raise (1/2) to higher powers:
- (1/2)³ = (1/2) × (1/2) × (1/2) = 1/8
- (1/2)⁴ = (1/2) × (1/2) × (1/2) × (1/2) = 1/16
We observe a pattern: as the exponent increases, the resulting fraction's numerator remains 1, while the denominator becomes a successively higher power of 2.
Let's also consider the implications of negative exponents:
- (1/2)⁻¹ = 2 (The reciprocal of 1/2)
- (1/2)⁻² = 4 (The reciprocal of (1/2)², which is 1/4)
Negative exponents essentially represent the reciprocal of the base raised to the positive power of the exponent.
Visualizing the Power of Fractions
Understanding fractions raised to powers can be made easier with visualization. Consider the concept of area. If we have a square with sides of length 1, its area is 1 x 1 = 1 square unit.
Now, let's consider a square with sides of length 1/2. Its area will be (1/2) x (1/2) = 1/4 square units. This visually demonstrates how raising 1/2 to the power of 2 results in 1/4.
This visualization technique can be extended to understand higher powers as well. Imagine dividing the initial square repeatedly into smaller and smaller squares, each representing a fraction of the original area.
Applications in Real-World Scenarios
Understanding fractional exponents has numerous real-world applications across various fields:
- Finance: Compound interest calculations rely heavily on exponential functions, including fractional exponents, to determine the growth of investments over time.
- Physics: Many physical phenomena, such as radioactive decay or the damping of oscillations, are modeled using exponential functions with fractional exponents.
- Computer Science: Algorithmic complexity analysis often employs exponential notation, including fractional exponents, to describe the efficiency of algorithms.
- Engineering: Fractional exponents appear in various engineering calculations related to scaling, stress, and strain in materials.
Conclusion: Mastering the Fundamentals
The seemingly simple problem of calculating (1/2)² opens up a vast landscape of mathematical concepts. Mastering the fundamentals of exponents, particularly fractional exponents, is crucial for tackling more complex problems in various fields. By understanding the underlying principles and applying the methods described here, you'll be well-equipped to handle similar calculations and build a strong foundation in mathematics. The ability to visualize these concepts, through areas or other representations, can further solidify your understanding and improve your problem-solving skills. Remember, mathematical proficiency is built incrementally, with each small step contributing to a greater understanding of the mathematical world.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 1/2 To The Power Of 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.